soda-official

外观

Chapter 1 质点运动学

约 3641 字大约 12 分钟

2025-09-18

Part 0 基础知识总结

· 位移 速度 加速度

位置矢量（位矢）：建立直角坐标系后，物体的位置可用坐标 A(x,y,z)A(x,y,z) 表示，向量 r⃗=OA→\vec{r}=\overrightarrow{OA} 就称为位置矢量，也记为 r⃗=xi⃗+yj⃗+zk⃗\vec{r}=x\vec{i}+y\vec{j}+z\vec{k} .

运动函数：运动函数就是质点坐标 x,y,zx,y,z 随 tt 的变化关系，将 tt 消掉判断运动轨迹

位移和路程：

  • 物体的位置变化称为位移 Δr⃗\Delta \vec{r} ，实际运动路径长称为路程 Δs\Delta s
  • Δr⃗\Delta \vec{r} 是位移，∣Δr⃗∣|\Delta \vec{r}| 是位移大小， Δr\Delta r 是物体到原点距离变化
  • 只有 ds=∣dr⃗∣ds=|d\vec{r}| 是正确的，出现 Δr\Delta r ， drdr 基本都是错的

速度：

  • 平均速度 v‾=Δr‾Δt\overline{v} = \frac{\Delta \overline{r}}{\Delta t}，平均速率是路程除以时间 v‾=ΔsΔt\overline{v} = \frac{\Delta s}{\Delta t}
  • 瞬时速度就是对每个坐标分量求导 v‾=dr‾dt=dxdti^+dydtj^+dzdtk^\overline{v} = \frac{d \overline{r}}{dt} = \frac{dx}{dt} \hat{i} + \frac{dy}{dt} \hat{j} + \frac{dz}{dt} \hat{k}
  • 瞬时速率是瞬时速度的大小

v=∣dr‾dt∣=dsdt=(dxdt)2+(dydt)2+(dzdt)2v = \left| \frac{d \overline{r}}{dt} \right| = \frac{ds}{dt} = \sqrt{\left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2 + \left( \frac{dz}{dt} \right)^2}

  • 注意：不能写成 drdt\frac{dr}{dt} 或 d∣r‾∣dt\frac{d|\overline{r}|}{dt}

加速度：

  • 平均加速度 a‾=Δv‾Δt\overline{a} = \frac{\Delta \overline{v}}{\Delta t}
  • 瞬时加速度就是对每个速度分量求导

a‾=dv‾dt=dvxdti^+dvydtj^+dvzdtk^\overline{a} = \frac{d \overline{v}}{dt} = \frac{dv_x}{dt} \hat{i} + \frac{dv_y}{dt} \hat{j} + \frac{dv_z}{dt} \hat{k}

  • 注意：加速度与速度同号为加速、异号为减速

转换：

v=dxdt,a=dvdtv=v0+∫0ta dt,x=x0+∫0tv dtv = \frac{dx}{dt}, \quad a = \frac{dv}{dt}\\ v = v_0 + \int_0^t a \, dt, \quad x = x_0 + \int_0^t v \, dt

· 圆周运动参数

加速度的分解：

  • 加速度可以沿速度方向分解

  • 与速度方向平行的称为切向加速度，改变速度的大小 at=dvdta_t = \frac{dv}{dt}

  • 与速度方向垂直的称为法向加速度，改变速度的方向 an=v2ρa_n = \frac{v^2}{\rho}（ρ\rho 为曲率半径）

转化：

角位移： $ \theta $ 角速度： ω\omega 角加速度： α\alpha

ω=dθdt,α=dωdt,ω=ω0+∫0tα dt,θ=θ0+∫0tω dt\omega = \frac{d\theta}{dt}, \quad \alpha = \frac{d\omega}{dt}, \quad \omega = \omega_0 + \int_0^t \alpha \, dt, \quad \theta = \theta_0 + \int_0^t \omega \, dt

角量与线量的关系：

  • 线速度 v=ωRv = \omega R

  • 法向加速度 an=v2R=ω2Ra_n = \frac{v^2}{R} = \omega^2 R

  • 切向加速度 at=dvdt=αRa_t = \frac{dv}{dt} = \alpha R

Part 1 质点

近代物理学研究的第一个课题是力学。这是由于它直接服务于战争的需要，即解释天体的运行和如何修正炮弹的弹道。为此，这一学科的研究得到了国王们的大力资助。

为了研究一个质点的运动，人们需要引入一个参照系。在这个参照系中，可以任取一点作为原点 OO，然后建立合适的坐标系。自然，如果原点取得不好，质点的运动方程可能写出来很复杂。除此之外，取什么样的参照系并不是什么大不了的问题。

在取定原点之后，我们可以从原点 OO 到质点 PP 画一向量（或矢量）

r=OP→,(1)\mathbf{r} = \overrightarrow{OP},\tag{1}

称为质点在该时刻的位置向量。显然，它是时间的函数，即我们有

r=r(t).(2)\mathbf{r} = \mathbf{r}(t).\tag{2}

在两个相邻时刻 tt 和 t+Δtt + \Delta t，粒子可能有两个不同的位置向量 r(t)\mathbf{r}(t) 和 r(t+Δt)\mathbf{r}(t + \Delta t)。它们的差 Δr(t)\Delta \mathbf{r}(t) 定义为

Δr(t)=r(t+Δt)−r(t).(3)\Delta \mathbf{r}(t) = \mathbf{r}(t + \Delta t) - \mathbf{r}(t).\tag{3}

由此，我们可以定义质点在时刻 tt 的速度为

v(t)≡lim⁡Δt→0Δr(t)Δt=drdt=r˙(t).(4)\mathbf{v}(t) \equiv \lim_{\Delta t \to 0} \frac{\Delta \mathbf{r}(t)}{\Delta t} = \frac{d\mathbf{r}}{dt} = \dot{\mathbf{r}}(t).\tag{4}

这是一个向量。它的绝对值

∣v∣≡v⋅v(5)|\mathbf{v}| \equiv \sqrt{\mathbf{v} \cdot \mathbf{v}}\tag{5}

被称为质点 PP 在时刻 tt 时的速率。

同理，我们可以定义质点在 tt 时刻的加速度向量为

a(t)≡lim⁡Δt→0Δv(t)Δt=lim⁡Δt→0v(t+Δt)−v(t)Δt=dv(t)dt=d2r(t)dt2.(6)\mathbf{a}(t) \equiv \lim_{\Delta t \to 0} \frac{\Delta \mathbf{v}(t)}{\Delta t} = \lim_{\Delta t \to 0} \frac{\mathbf{v}(t + \Delta t) - \mathbf{v}(t)}{\Delta t} = \frac{d\mathbf{v}(t)}{dt} = \frac{d^2\mathbf{r}(t)}{dt^2}.\tag{6}

用矢量来描述质点运动的好处是，对于给定的参照系，矢量表示的运动方程的形式与具体的坐标系的选择无关。因此，便于我们做一般性的定义陈述和理论推导。但是，在做具体计算时，我们还需要根据问题的特点，选择适当的坐标系。

Part 2 坐标系

· 直角坐标系

当质点的加速度为一个常向量时，选用直角坐标系往往是适宜的。在这一坐标系中，我们在原点上建立三个互相垂直的固定坐标轴。以 ex\mathbf{e}_x, ey\mathbf{e}_y 和 ez\mathbf{e}_z 表示沿这三个轴方向的单位向量，则我们有

ex⋅ey=ey⋅ez=ez⋅ex=0,(7)\mathbf{e}_x \cdot \mathbf{e}_y = \mathbf{e}_y \cdot \mathbf{e}_z = \mathbf{e}_z \cdot \mathbf{e}_x = 0,\tag{7}

以及

ex⋅ex=ey⋅ey=ez⋅ez=1.(8)\mathbf{e}_x \cdot \mathbf{e}_x = \mathbf{e}_y \cdot \mathbf{e}_y = \mathbf{e}_z \cdot \mathbf{e}_z = 1.\tag{8}

在这一坐标系下，质点的位置向量可以被写作

r(t)=x(t)ex+y(t)ey+z(t)ez.(9)\mathbf{r}(t) = x(t)\mathbf{e}_x + y(t)\mathbf{e}_y + z(t)\mathbf{e}_z.\tag{9}

而其速度和加速度向量可被分别写作

v(t)=dr(t)dt=ddt(x(t)ex+y(t)ey+z(t)ez)=(x˙(t)ex+x(t)dexdt+y˙(t)ey+y(t)deydt+z˙(t)ez+z(t)dezdt)=x˙(t)ex+y˙(t)ey+z˙(t)ez≡vx(t)ex+vy(t)ey+vz(t)ez,(10)\begin{aligned} \mathbf{v}(t) &= \frac{d\mathbf{r}(t)}{dt} = \frac{d}{dt} (x(t)\mathbf{e}_x + y(t)\mathbf{e}_y + z(t)\mathbf{e}_z) \\ &= \left( \dot{x}(t)\mathbf{e}_x + x(t)\frac{d\mathbf{e}_x}{dt} + \dot{y}(t)\mathbf{e}_y + y(t)\frac{d\mathbf{e}_y}{dt} + \dot{z}(t)\mathbf{e}_z + z(t)\frac{d\mathbf{e}_z}{dt} \right) \\ &= \dot{x}(t)\mathbf{e}_x + \dot{y}(t)\mathbf{e}_y + \dot{z}(t)\mathbf{e}_z \equiv v_x(t)\mathbf{e}_x + v_y(t)\mathbf{e}_y + v_z(t)\mathbf{e}_z, \end{aligned}\tag{10}

以及

a(t)=dv(t)dt=v˙x(t)ex+v˙y(t)ey+v˙z(t)ez=d2x(t)dt2ex+d2y(t)dt2ey+d2z(t)dt2ez≡ax(t)ex+ay(t)ey+az(t)ez.(11)\begin{align*} \mathbf{a}(t) &= \frac{d\mathbf{v}(t)}{dt} = \dot{v}_x(t)\mathbf{e}_x + \dot{v}_y(t)\mathbf{e}_y + \dot{v}_z(t)\mathbf{e}_z\\ &= \frac{d^2 x(t)}{dt^2}\mathbf{e}_x + \frac{d^2 y(t)}{dt^2}\mathbf{e}_y + \frac{d^2 z(t)}{dt^2}\mathbf{e}_z\\ & \equiv a_x(t)\mathbf{e}_x + a_y(t)\mathbf{e}_y + a_z(t)\mathbf{e}_z. \end{align*}\tag{11}

· 极坐标系

当质点所受到的力总是指向参照系原点时，使用所谓极坐标系是比较方便的。

首先，我们从原点 OO 引出一根固定的轴，称为极轴。然后再做从原点 OO 到质点 PP 的连线 r\mathbf{r}。则质点 PP 的位置可以由两个参数

r=(r,θ).(12)\mathbf{r} = (r, \theta).\tag{12}

给定。这里，rr 为质点到原点的距离，而 $ \theta $ 则为 r\mathbf{r} 与极轴之间的夹角。为了计算的缘故，我们再引入两个互相垂直的单位向量。其中，er\mathbf{e}_r 是沿 r\mathbf{r} 的方向，而 eθ\mathbf{e}_\theta 则沿角度 $ \theta $ 增大的方向。

需要强调一点的是，er\mathbf{e}_r 和 eθ\mathbf{e}_\theta 都不是常向量。因此，我们需要计算它们随时间的变化率 e˙r\dot{\mathbf{e}}_r 和 e˙θ\dot{\mathbf{e}}_\theta。首先，不难看到，我们有

Δer(t)=er(t+Δt)−er(t)≈1⋅Δθ⋅eθ.(13)\Delta \mathbf{e}_r(t) = \mathbf{e}_r(t + \Delta t) - \mathbf{e}_r(t) \approx 1 \cdot \Delta \theta \cdot \mathbf{e}_\theta.\tag{13}

因此，e˙r\dot{\mathbf{e}}_r 可以被写作

derdt=lim⁡Δt→0ΔerΔt=lim⁡Δt→0ΔθΔt⋅eθ=θ˙eθ.(14)\frac{d \mathbf{e}_r}{dt} = \lim_{\Delta t \to 0} \frac{\Delta \mathbf{e}_r}{\Delta t} = \lim_{\Delta t \to 0} \frac{\Delta \theta}{\Delta t} \cdot \mathbf{e}_\theta = \dot{\theta} \mathbf{e}_\theta.\tag{14}

同理，我们有

Δeθ(t)=eθ(t+Δt)−eθ(t)≈1⋅Δθ⋅(−er).(15)\Delta \mathbf{e}_\theta(t) = \mathbf{e}_\theta(t + \Delta t) - \mathbf{e}_\theta(t) \approx 1 \cdot \Delta \theta \cdot (-\mathbf{e}_r).\tag{15}

因此，取极限后，我们得到

deθdt=lim⁡Δt→0ΔeθΔt=lim⁡Δt→0ΔθΔt⋅(−er)=−θ˙er.(16)\frac{d \mathbf{e}_\theta}{dt} = \lim_{\Delta t \to 0} \frac{\Delta \mathbf{e}_\theta}{\Delta t} = \lim_{\Delta t \to 0} \frac{\Delta \theta}{\Delta t} \cdot (-\mathbf{e}_r) = -\dot{\theta} \mathbf{e}_r.\tag{16}

这两个公式是我们今后常要用到的。

现在，我们可以将质点速度和加速度向量在极坐标下的形式写出。它们分别为

v=r˙=ddt(rer)=r˙er+re˙r=r˙er+rθ˙eθ.(17)\mathbf{v} = \dot{\mathbf{r}} = \frac{d}{dt} (r \mathbf{e}_r) = \dot{r} \mathbf{e}_r + r \dot{\mathbf{e}}_r = \dot{r} \mathbf{e}_r + r \dot{\theta} \mathbf{e}_\theta.\tag{17}

以及

a=v˙=ddt(r˙er+rθ˙)=(d2rdt2er+r˙e^r+r˙θ˙eθ+rd2θdt2eθ+rθ˙e^θ)=(d2rdt2er+r˙θ˙eθ+r˙θ˙eθ+rd2θdt2eθ−rθ˙2er)=(d2rdt2−rθ˙2)er+(2r˙θ˙+rd2θdt2)eθ.(18)\begin{align*} \mathbf{a}& = \dot{\mathbf{v}} = \frac{d}{dt} \left( \dot{r} \mathbf{e}_r + r \dot{\theta}\right)\\ &= \left( \frac{d^2r}{dt^2} \mathbf{e}_r + \dot{r} \mathbf{\hat{e}}_r + \dot{r}\dot{\theta} \mathbf{e}_{\theta} + r \frac{d^2\theta}{dt^2} \mathbf{e}_{\theta} + r \dot{\theta} \mathbf{\hat{e}}_{\theta} \right)\\ &= \left( \frac{d^2r}{dt^2} \mathbf{e}_r + \dot{r}\dot{\theta} \mathbf{e}_{\theta} + \dot{r}\dot{\theta} \mathbf{e}_{\theta} + r \frac{d^2\theta}{dt^2} \mathbf{e}_{\theta} - r \dot{\theta}^2 \mathbf{e}_r \right)\\ &= \left( \frac{d^2r}{dt^2} - r \dot{\theta}^2 \right) \mathbf{e}_r + \left( 2 \dot{r} \dot{\theta} + r \frac{d^2\theta}{dt^2} \right) \mathbf{e}_{\theta}. \end{align*}\tag{18}

这些表达式中，er\mathbf{e}_r 方向的分量被称为径向速度和径向加速度。而 eθ\mathbf{e}_{\theta} 方向的分量则被称为横向速度和横向加速度。同时，θ˙\dot{\theta} 和 d2θdt2\frac{d^2\theta}{dt^2} 被称为质点的角速度和角加速度。

· 例题

/example/

在离地面不远处，一个质点运动的加速度是指向地心的。当该质点的横向速度为何时，它做一圆周运动，从而成为地球的卫星？

/solution/

当质点做匀速圆周运动时，其横向加速度 aθa_{\theta} 为零，而其径向加速度为

a=g=−ger.\mathbf{a} = \mathbf{g} = -g \mathbf{e}_r.

因此，在以地心为原点的极坐标系中，我们有

d2rdt2−rθ˙2=−g,rd2θdt2+2r˙θ˙=0.\frac{d^2r}{dt^2} - r \dot{\theta}^2 = -g, \quad r \frac{d^2\theta}{dt^2} + 2 \dot{r} \dot{\theta} = 0.

特别是，在这一运动中，r=Rr = R 为一常数。因此上式中，rr 对于时间的一次和二次导数皆为零。故上式退化为

Rθ˙2=g,Rd2θdt2=0.R \dot{\theta}^2 = g, \quad R \frac{d^2\theta}{dt^2} = 0.

从第二个方程中，我们解得

θ˙=constant.\dot{\theta} = constant.

从第一个方程中，我们得到

(Rθ˙)2R=g.\frac{(R \dot{\theta})^2}{R} = g.

又由于 Rθ˙R \dot{\theta} 为质点绕地球运动的横向速度 vθv_{\theta} 。因此，我们最后得到

vθ2=gR,v_{\theta}^2 = gR,

或是

vθ=gR.v_{\theta} = \sqrt{gR}.

将

g=980 cm/s2,R≈6.37×108 cmg = 980 \, \text{cm/s}^2, \quad R \approx 6.37 \times 10^8 \, \text{cm}

代入上面的方程后，我们得到

vθ=980×6.37×108≈64×1010=8×105 cm/s=8 km/sv_{\theta} = \sqrt{980 \times 6.37 \times 10^8} \approx \sqrt{64 \times 10^{10}} = 8 \times 10^5 \, \text{cm/s} = 8 \, \text{km/s}

这一速度称为第一宇宙速度。

· 自然坐标系

在理论推导中，采用所谓自然坐标系常会带来很大的便利。我们今后也会经常用到它。

如图所示，我们先取质点运动轨迹上的任一点作为起始位置，对应的时间为 t=0t = 0 。

在此之后 (t>0)(t > 0) ，质点所到达的任何一点 PP 的坐标由其从起始点算起的弧长 ss 决定。

在 PP 点处，我们可以取曲线的切线方向的单位向量 τ⃗\vec{\tau} 和内法线方向单位向量 n⃗\vec{n} 。它们就定义了所谓自然坐标系。

显然，这样定义的 τ⃗\vec{\tau} 和 n⃗\vec{n} 都不是常向量。在轨迹的不同位置，我们有不同的 τ⃗\vec{\tau} 和 n⃗\vec{n} 。

/

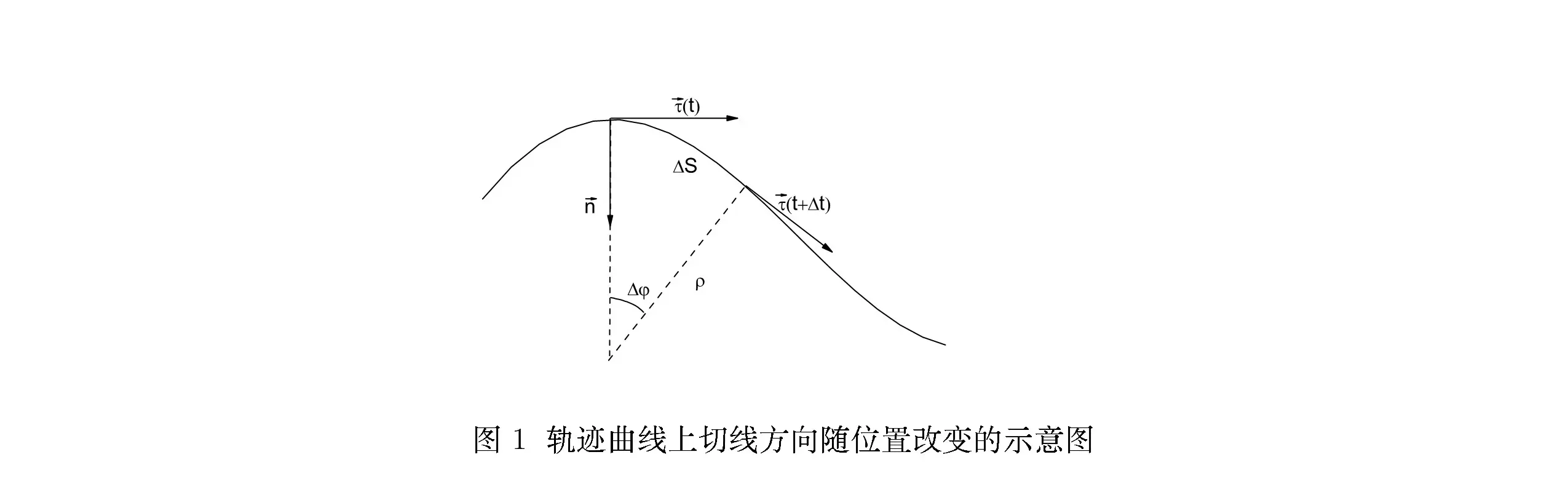
设在 tt 和 t+Δtt + \Delta t 时刻，质点的位置分别为 r(t)\mathbf{r}(t) 及 r(t+Δt)\mathbf{r}(t + \Delta t) 。而它们对应的从起始点计算的弧长为 s(t)s(t) 和 s(t+Δt)s(t + \Delta t) ，并且两点间的向量差为 Δr\Delta \mathbf{r} 。则从微分几何学中，我们知道

τ⃗=lim⁡Δs→0Δτ⃗Δs=drds\vec{\tau} = \lim_{\Delta s \to 0} \frac{\Delta \vec{\tau}}{\Delta s} = \frac{d\mathbf{r}}{ds}

成立。进一步，我们还有

dτ⃗ds=lim⁡Δs→0Δτ⃗Δs=lim⁡Δs→0Δτ⃗Δφ⋅lim⁡Δs→0ΔφΔs=1ρn⃗.\frac{d\vec{\tau}}{ds} = \lim_{\Delta s \to 0} \frac{\Delta \vec{\tau}}{\Delta s} = \lim_{\Delta s \to 0} \frac{\Delta \vec{\tau}}{\Delta \varphi} \cdot \lim_{\Delta s \to 0} \frac{\Delta \varphi}{\Delta s} = \frac{1}{\rho} \vec{n}.

这里， ρ\rho 称为曲线在 r\mathbf{r} 处的密切圆曲率半径。在图1中，我们给出了这些几何关系的一个示意图。下面，我们还要用到它们。

现在，让我们回过头来看一下，质点随时间改变的速度和加速度如何在自然坐标系中给出。

按照定义，我们有

v=drdt=drds⋅dsdt=dsdtτ⃗=vτ⃗.\mathbf{v} = \frac{d\mathbf{r}}{dt} = \frac{d\mathbf{r}}{ds} \cdot \frac{ds}{dt} = \frac{ds}{dt} \vec{\tau} = v \vec{\tau}.

这里， vv 称为质点的切向速率。从上式中我们可以看到，质点的速度永远是沿着切线方向的。

/

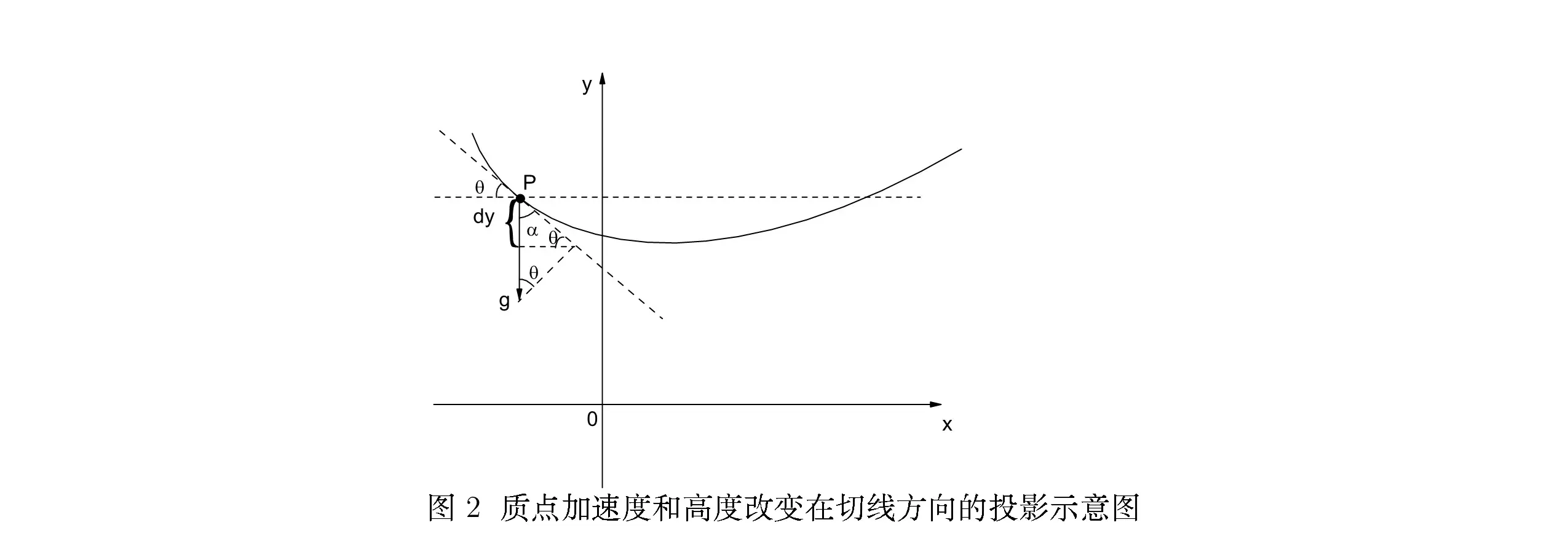
至于加速度 a\mathbf{a} ，我们可以计算如下。

a=dvdt=ddt(vτ⃗)=dvdtτ⃗+vdτ⃗dt\mathbf{a} = \frac{d\mathbf{v}}{dt} = \frac{d}{dt}(v\vec{\tau}) = \frac{dv}{dt}\vec{\tau} + v\frac{d\vec{\tau}}{dt}

=dvdtτ⃗+vdτ⃗ds⋅dsdt=dvdtτ⃗+v⋅vρn⃗= \frac{dv}{dt}\vec{\tau} + v\frac{d\vec{\tau}}{ds} \cdot \frac{ds}{dt} = \frac{dv}{dt}\vec{\tau} + v \cdot \frac{v}{\rho} \vec{n}

=dvdtτ⃗+v2ρn⃗≡aττ⃗+ann⃗.= \frac{dv}{dt}\vec{\tau} + \frac{v^2}{\rho} \vec{n} \equiv a_\tau \vec{\tau} + a_n \vec{n}.

这里，

aτ=dvdt,an=v2ρa_\tau = \frac{dv}{dt}, \quad a_n = \frac{v^2}{\rho}

分别为质点的切向和法向加速度分量。

Part 3 相对运动

· 伽利略变换

在实际工作中，如何选取参照系往往是由观察环境决定的。例如，为了描述太阳系中物体的运动，最好选取太阳为坐标的原点。然而，为了描述地球上的一辆汽车或一艘轮船的运动，这样的选取显然是不明智的。此时，我们最好选取地球上的一个固定点，例如地心作为原点。这样，就导致了一个间题，即如何在两个不同的参照系中，描述同一个物体的运动。

为了回答这一问题，让我们考虑如下的例子。假设一个参照系 S′S' 相对于另外一个参照系 SS 做运动。而空间中又有一个质点 PP 相对于二者运动。显然，我们有

r=r′+R.(1)\mathbf{r} = \mathbf{r'} + \mathbf{R}. \tag{1}

这里， r\mathbf{r} 和 r′\mathbf{r'} 分别是质点 PP 相对于 SS 系的原点 OO 和 S′S' 系的原点 O′O' 的矢径。而 R\mathbf{R} 则为 O′O' 相对于 OO 的位置向量。

在非相对论力学中，我们假定时间是不随参照系的选取而改变的。即我们有

t′=t.(2)t' = t. \tag{2}

将方程 (1) 和方程 (2) 联立后，我们既得到所谓的 Galileo 变换。

现在将方程 (1) 两边对时间求导后，我们有

vP=r˙=R˙+r˙′=Ve+vP′.(3)\mathbf{v}_P = \dot{\mathbf{r}} = \dot{\mathbf{R}} + \dot{\mathbf{r}}' = \mathbf{V}_{e} + \mathbf{v}_P'. \tag{3}

这里， vP\mathbf{v}_P 和 vP′\mathbf{v}_P' 分别为质点相对于参照系 SS 和 S′S' 的速度，而 Ve\mathbf{V}_{e} 则称为两个参照系之间的牵连速度。

同理，对于质点的加速度，我们有

aP=v˙P=V˙e+v˙P′=Ae+aP′.(4)\mathbf{a}_P = \dot{\mathbf{v}}_P = \dot{\mathbf{V}}_{e} + \dot{\mathbf{v}}_P' = \mathbf{A}_{e} + \mathbf{a}_P'. \tag{4}

结束.

更新日志

2025/10/13 08:58
查看所有更新日志
  • 375bf-delete于
  • c9ee8-plume于
  • a28aa-a于

版权归属：nicostore-mathematica

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)