概率论

约 6022 字大约 20 分钟

2025-09-17

Part 1 基本公式

· 随机事件

(1) 随机试验：在概率论中将具备下列三个条件的试验称为随机试验，简称试验：

在相同条件下可重复进行；
每次试验的结果具有多种可能性；
在每次试验之前不能准确预言该次试验将出现何种结果，但是所有结果明确可知。

(2) 样本空间：随机试验的所有可能结果构成的集合，常用 Ω 表示。

(3) 随机事件：随机试验的每一种可能的结果称为随机事件，常用 A, B, C, D 表示。

(4) 基本事件：不能分解为其他事件组合的最简单的随机事件。

(5) 必然事件：每次试验中一定发生的事件，常用 Ω 表示。

(6) 不可能事件：每次试验中一定不发生的事件，常用 $\varnothing$ 表示。

/Definition/
事件的关系及运算：
(1) 包含：若 $A$ 发生必然导致 $B$ 发生，则称 $A$ 包含于 $$B$$，记为 $A \subset B$
(2) 相等：若 $A \subset B$ 且 $B \subset A$ ，则称 $A$ 与 $B$ 相等，记为 $A = B$
(3) 事件的和： A 与 B 至少有一个发生，称为 A 与 B 的和事件，记为 $A \cup B$
(4) 事件的积： A 与 B 同时发生，称为 A 与 B 的积事件，记为 $A \cap B$ （或 AB）
(5) 事件的差： A 发生而 B 不发生，称为 A 与 B 的差事件，记为 $A - B$
(6) 互斥事件：在试验中，若事件 A 与 B 不能同时发生，即 $A \cap B = \varnothing$ ，则称 A, B 为互斥事件，或互不相容事件。
(7) 对立事件：在每次试验中，“事件 A 不发生”的事件称为事件 A 的对立事件或逆事件。A 的对立事件常记为 $\overline{A}$ 。

· 概率定义

高中阶段我们接触过概率的统计学定义：
在相同的条件下，重复进行 $n$ 次试验，事件 $A$ 发生的频率稳定在某一常数 $p$ 附近摆动，且一般说来， $n$ 越大，摆动幅度越小，则称常数 $p$ 为事件 $A$ 的概率，记为 $P(A)$ .
下面我们尝试将概率公理化：

设 Ω 是一样本空间，称满足下列三条公理的集函数 $P(\cdot)$ 为定义在 Ω 上的概率：

非负性：任何事件的概率都不是负数， $P(A)\geq0$ 。
可加性：如果事件 $A_{1}$ 、 $A_{2}$ 、 $\cdots$ 、 $A_{n}$ 互斥，则
$P(A_{1}\cup A_{2}\cup\cdots\cup A_{n})=P(A_{1})+P(A_{2})+\cdots+P(A_{n})$ $P(\bigcup_{i=1}^{\infty} A_i) = \sum_{i=1}^{\infty} P(A_i)$
归一性：整个样本空间也被称为必然事件，它的概率为 $1$ ， $P(\Omega)=1$ 。

· 运算性质

(1) 加法律

P(A\cup B)=P(A)+P(B)-P(A\cap B)

加法公式还能推广到多个事件的情况，例如，设 $A_1, A_2, A_3$ 为任意三个事件，则有
$P(A_1 \cup A_2 \cup A_3) = P(A_1) + P(A_2) + P(A_3) - P(A_1A_2) - P(A_1A_3) - P(A_2A_3) + P(A_1A_2A_3)$
一般地，对于任意 n 个事件 $A_1, A_2, \cdots, A_n$ ，有
$P(A_1 \cup A_2 \cup \cdots \cup A_n) = \sum_{i=1}^{n} P(A_i) - \sum_{1 \leq i < j \leq n} P(A_iA_j) + \sum_{1 \leq i < j < k \leq n} P(A_iA_jA_k) + \cdots + (-1)^{n+1} P(A_1A_2 \cdots A_n)$

(2) 减法律

P(\overline{A})=1-P(A)\\ P(A-B)=P(A)-P(A\cap B)

(3) 结合律

A\cap(B\cap C)=(A\cap B)\cap C\\ A\cup(B\cup C)=(A\cup B)\cup C

(4) 分配律

A\cap(B\cup C)=(A\cap B)\cup(A\cap C) A\cup(B\cap C)=(A\cup B)\cap(A\cup C)

(5) 补集定律（德摩根定律）

\overline{A\cap B}=\overline{A}\cup\overline{B}

（只要不同时在A，B里就行）可推广： $\overline{A\cap B\cap C}=\overline{A}\cup\overline{B}\cup\overline{C}$

\overline{A\cup B}=\overline{A}\cap\overline{B}

（既不能在A里也不能在B里）可推广：
$\overline{A\cup B\cup C}=\overline{A}\cap\overline{B}\cap\overline{C}$

· 条件概率公式

公式:

P(A|B)=\frac{P(AB)}{P(B)}

或等价形式

P(AB)=P(A|B)P(B)

拓展（多事件链式公式）: 对于事件序列 $A_{1},A_{2},...,A_{n}$ ：

P(A_{1}\cap A_{2}\cap...\cap A_{n})=P(A_{1})\cdot P(A_{2}\mid A_{1})\cdot P(A_{3}\mid A_{1}\cap A_{2})\cdots P(A_{n}\mid A_{1}\cap A_{2}\cap...A_{n-1})

· 贝叶斯公式

若 $B_{1},B_{2},...,B_{n}$ 构成完备事件组（两两互斥且并集为样本空间），则：

全概率公式:

P(A)=\sum_{i=1}^{n}P(B_{i})P(A|B_{i})

贝叶斯公式:

P(B_{k}|A)=\frac{P(B_{k})P(A|B_{k})}{P(A)}

事件 $A$ 和 $B$ 如果发生的因果关系极小（互不影响），则称 $A$ 与 $B$ 为独立事件。
此时满足： 概率乘法公式:
$P(A \cap B) = P(A) \cdot P(B)$
条件概率等价表述:
$P(A \mid B) = P(A) \\ P(B \mid A) = P(B)$

· 古典概型

样本空间由 $n$ 个等可能的基本事件构成，具有下列两个特点的试验称为古典概型：

(1) 每次试验只有有限种可能的试验结果。

(2) 每次试验中，各基本事件出现的可能性完全相同。

对于古典概型，事件 A 发生的概率为

P(A)=\frac{\text{The number of basic events contained in event}\ A}{n}

· 几何概型

如果随机试验的样本空间是一个区域（例如直线上的区间、平面或空间中的区域），而且样本空间中每个试验结果的出现具有等可能性，那么规定事件 A 的概率为：

P(A)=\frac{\mu (A)}{\mu(\Omega)}

· 事件独立性

如果事件 A 发生的可能性不受事件 B 发生与否的影响，也就是 $P(A | B) = P(A)$ ，则称事件 A 对于事件 B 独立。若 A 对于 B 独立，则 B 对于 A 也独立，那么就称事件 A 与事件 B 相互独立。

基本性质：
(1) A 与 B 相互独立 $\Leftrightarrow P(AB) = P(A)P(B)$ 。
(2) 若 A 与 B 相互独立，则 $A \cap \overline{B}, \overline{A} \cap B, \overline{A} \cap \overline{B}$ 中的每一对事件都相互独立。

针对 $n$ 个事件相互独立： $n(n > 2)$ 个事件 $A_1, A_2, \cdots, A_n$ 中任意一个事件发生的可能性都不受其他一个或多个事件发生与否的影响，则称 $A_1, A_2, \cdots, A_n$ 相互独立。

基本性质：
(1) 如果事件 $A_1, A_2, \cdots, A_n$ 相互独立，则对于任意 $k (1 \leq k \leq n)$ 和任意 $1 \leq i_1 < i_2 < \cdots < i_k \leq n$ ， $P(A_{i_1}A_{i_2} \cdots A_{i_k}) = P(A_{i_1})P(A_{i_2}) \cdots P(A_{i_k})$ 成立。
(2) 如果事件 $A_1, A_2, \cdots, A_n$ 相互独立，则将 $A_1, A_2, \cdots, A_n$ 中任意多个事件换成它们的逆事件，所得的 $n$ 个事件仍相互独立。
(3) 如果事件 $A_1, A_2, \cdots, A_n$ 相互独立，则
$P\left(\bigcup_{i=1}^{n} A_i\right) = 1 - \prod_{i=1}^{n} P(\overline{A_i})。$

· 重复独立试验

在 $n$ 次试验中，若任意一次试验的诸结果是相互独立的，则称这 $n$ 次试验为重复独立试验或独立试验序列。

(1) 伯努利概型：假定一次试验中只有事件 $A$ 发生或 $\overline{A}$ 发生，每次试验的结果与其他各次试验结果无关，这样的 $n$ 次重复试验称为 $n$ 重伯努利试验或伯努利概型。
(2) 二项概率公式：设一次试验中事件 $A$ 发生的概率为 $p (0 < p < 1)$ ，则在 $n$ 重伯努利试验中，事件 $A$ 恰好发生 $k$ 次的概率为 $P_n(k) = C_n^k p^k q^{n-k}$ ， $k = 0, 1, \cdots, n$ ，其中 $q = 1 - p$ 。

Part 2 一维随机变量

· 随机变量

看下面几个例子：

（1）掷骰子：掷一次普通的六面骰子，将出现的点数记为𝑐。
（2）投硬币：投掷 100 次硬币，统计正面出现的次数，记为𝑎。
（3）班级人数：在一个学校里随机选择一个班级，将学生人数记为𝑛。
（4）身高：测量一群人的身高，将结果记为ℎ。
（5）重量：记录某个产品的质量，将结果记为𝑚。
（6）时间：记录一个运动员跑 100 米的时间为𝑡。

随机变量是实验结果的实值函数：将实验结果与某个实数绑定。

而随机变量可根据分布特点划为两种情况：离散随机变量和连续随机变量。

除了一维变量，还常见二维变量，比如：

（1）考试成绩：将学生的英语分数𝑎和数学分数𝑏记录为一个二维数据(𝑎, 𝑏)。
（2）温度湿度：将城市中一天内的平均温度𝑇与湿度𝑊记录为一个二维数据(𝑇, 𝑊)。

· 定义

设 E 是一个随机试验，其样本空间为 $\Omega={\omega}$ ，如果对于每一个样本点 $\omega \in \Omega$ ，都有唯一的一个实数 $X(\omega)$ 与之对应，则称 $X(\omega)$ 为一维随机变量。通常用 $X, Y, Z, \cdots$ 表示随机变量。

分布函数

设 $X$ 是一个随机变量， $x$ 是任意实数，则函数 $F(x)=P\{X\leq x\}$ 称为 $X$ 的分布函数。

(1) 单调性: $F(x)$ 是一个单调不减的函数，即当 $x_1<x_2$ 时， $F(x_1)\leq F(x_2)$ 。
(2) 有界性: $0\leq F(x)\leq 1$ ，且
$F(+\infty)=\lim_{x\to +\infty} F(x)=1,\quad F(-\infty)=\lim_{x\to -\infty} F(x)=0.$
(3) 右连续性: $F(x+0)=F(x)$ ，即 $F(x)$ 是右连续函数。

由分布函数求概率

P\{a<X\leq b\}=P\{X\leq b\}-P\{X\leq a\}=F(b)-F(a).

· 一维离散变量

· 0-1分布

其分布律为

X	0	1
P	p	1-p

其中 $p$ 为事件 $A$ 出现的概率， $0 < p < 1$ 。

· 二项分布

若实验仅有两种结果 $A$ 和 $\overline{A}$ ，且 $P(A)=p$ 。将该实验独立重复 $n$ 次，事件 $A$ 发生的次数 $X$ 服从二项分布，

其概率分布律为：

P(X=k)=C_{n}^{k}p^{k}(1-p)^{n-k}=\frac{n(n-1)\cdots(n-k+1)}{k!}p^{k}(1-p)^{n-k}

记法:

X\sim b(n,p)

· 泊松分布

当二项分布中 $n \geq 20$ 且 $p \leq 0.05$ 时，可用泊松分布近似，其概率公式为：

P(X=k)=\frac{\lambda^{k}}{k!}e^{-\lambda} \quad (\lambda=np)

记法：

X\sim \pi(\lambda)

拓展知识：当𝝀越来越大时，泊松分布曲线越发接近正态分布。

关于泊松分布的由来：

当二项分布 $X \sim b(n,p)$ 满足 $n \to +\infty$ 且记 $\lambda = np$ 时：
$P(X=k)=\lim_{n \to \infty} C_n^k p_n^k (1 - p_n)^{n-k}=\lim _{n\rightarrow+\infty}\frac{n(n-1)\cdots(n-k+1)}{k!}p^{k}(1-p)^{n-k}=\frac{\lambda^{k}}{k!}e^{-\lambda}$
通过泰勒展开式验证所有概率之和为1：
$\mathrm{e}^{x}=\sum_{k=0}^{n}\frac{x^{k}}{k!}=1+\frac{x}{1!}+\frac{x^{2}}{2!}+\cdots+\frac{x^{n}}{n!}$
概率求和:
$\sum_{k=0}^{n}P(X=k)=\sum_{k=0}^{n}\frac{\lambda^{k}}{k!}e^{-\lambda}=e^{-\lambda}\cdot e^{\lambda}=1$

· 超几何分布

设随机变量 $X$ 的分布律是

P\{X = i\} = \frac{C_M^i C_{N-M}^{n-i}}{C_N^n} \quad (i = 0, 1, 2, \cdots, l; \, l = \min\{n, M\}),

其中 $M, N, n$ 都是自然数，且 $n < N, M < N$ ，则称 $X$ 服从参数为 $N, M, n$ 的超几何分布，记作 $X \sim H(N, M, n)$ 。

· 几何分布

设随机变量 $X$ 的分布律为

P\{X = i\} = (1 - p)^{i-1} p, \quad i = 1, 2, \cdots,

其中 $0 < p < 1$ ，则称 $X$ 服从参数为 $p$ 的几何分布，记为 $X \sim G(p)$ 。

· 一维连续变量

设想以下几种情况：

（1）让一辆车随机停在街边的某个位置，坐标记为 $𝑥$ 。

（2）一个运动员跑 100 米所需的时间，记为 $𝑡$ 。

如何描述随机变量 $𝑥$ 和 $𝑡$ 的取值情况？需要认识什么是概率密度函数。

设 $X$ 是一个连续随机变量， $x$ 是任意实数：

概率密度函数 (PDF)

f(x)=\lim_{\Delta x\to 0}\frac{P(x\leq X\leq x+\Delta x)}{\Delta x}

概率分布函数 (CDF)

F(x)=P(X\leq x)

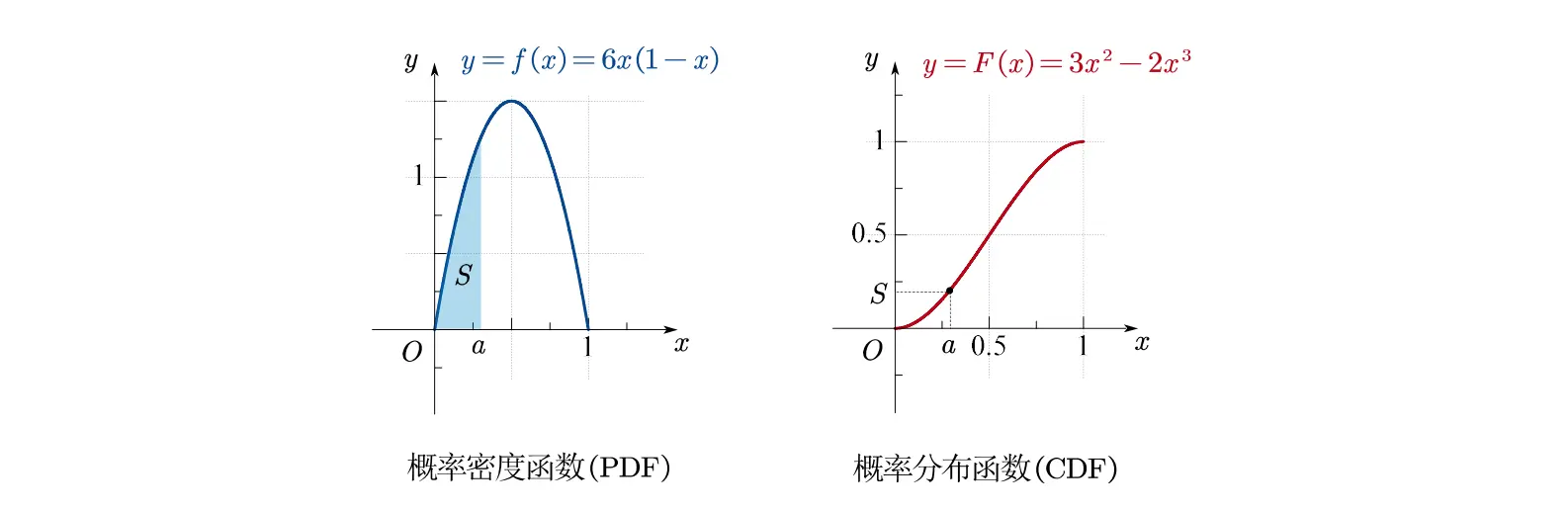
特性	密度函数 $f(x)$	分布函数 $F(x)$
两端	$x\to\infty,\ f(x)\to 0$	$x\to -\infty,\ F(x)\to 0$ $x\to +\infty,\ F(x)\to 1$
单调性	不一定	单调递增
阴影面积	$\int_{-\infty}^{+\infty} f(x)dx=1$	不一定
应用场景	关注特定区间的概率情况	关注左侧 ( $\leq$ ) 的整体累积情况
关联	$F'(x)=f(x)$	$\int_{-\infty}^{x} f(t)dt=F(x)$

· 均匀分布

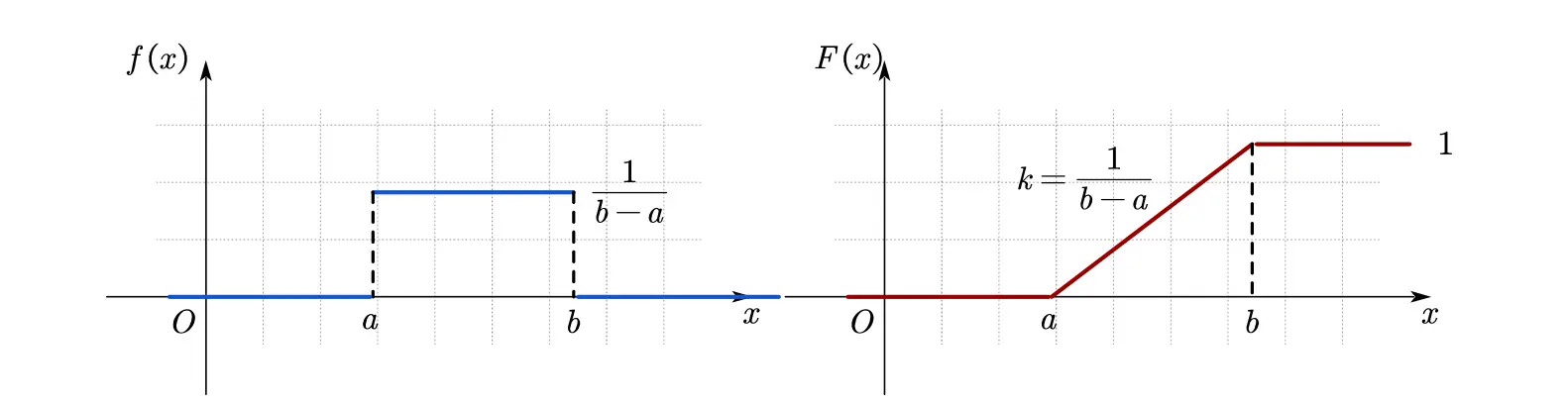
概率密度函数 (PDF):

f(x)=\begin{cases} \frac{1}{b-a}, & a\leq x\leq b \\ 0, & \text{others} \end{cases}

概率分布函数 (CDF):

F(x)=\begin{cases} 0, & x<a \\ \frac{x-a}{b-a}, & a\leq x\leq b \\ 1, & x>b \end{cases}

期望:

\mu=\frac{a+b}{2}

方差:

\sigma^2=\frac{(b-a)^2}{12}

· 正态分布

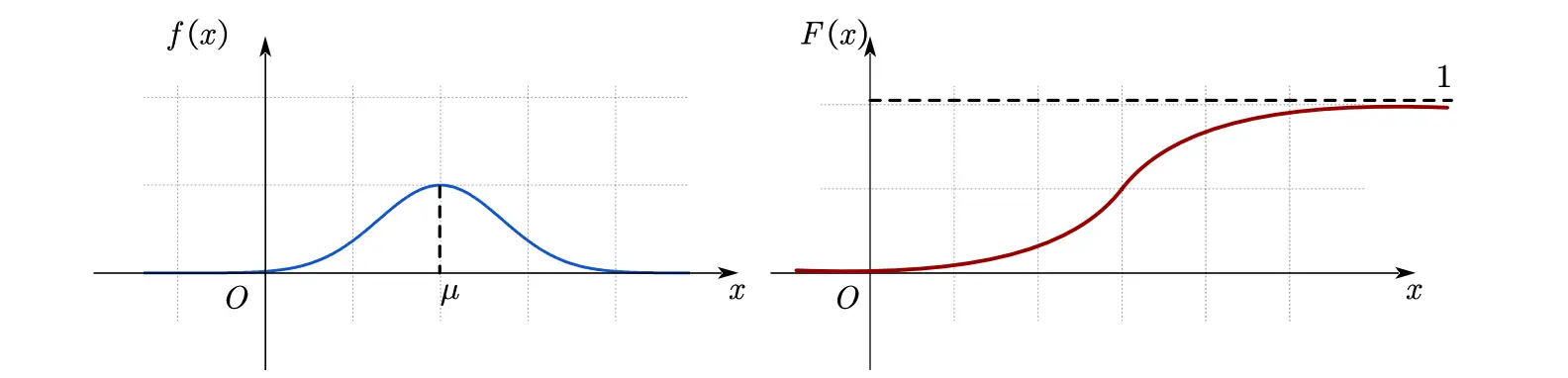
概率密度函数 (PDF):

\phi(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\quad (x\in\mathbb{R})

概率分布函数 (CDF):

\Phi(x)=\frac{1}{2}\left[1+\mathrm{erf}\left(\frac{x-\mu}{\sigma\sqrt{2}}\right)\right]

期望: $\mu$ 方差: $\sigma^2$ .

标准正态分布：当 $\mu = 0,\quad \sigma = 1$ 时称 $X$ 服从标准正态分布，简记为 $X \sim N(0, 1)$ ，其概率密度函数和分布函数分别用 $\varphi(x), \Phi(x)$ 表示，即有

\varphi(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \quad

\Phi(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{x} e^{-\frac{t^2}{2}} dt.

性质 1
$\Phi(-x) = 1 - \Phi(x)$
性质 2 ：当 $X \sim N(\mu, \sigma^2)$ 时， $U = \frac{X - \mu}{\sigma} \sim N(0, 1)$ ，即
$F(x) = \Phi\left(\frac{x - \mu}{\sigma}\right)$
可把一般正态分布化为标准正态分布 $N(0, 1)$

· 指数分布

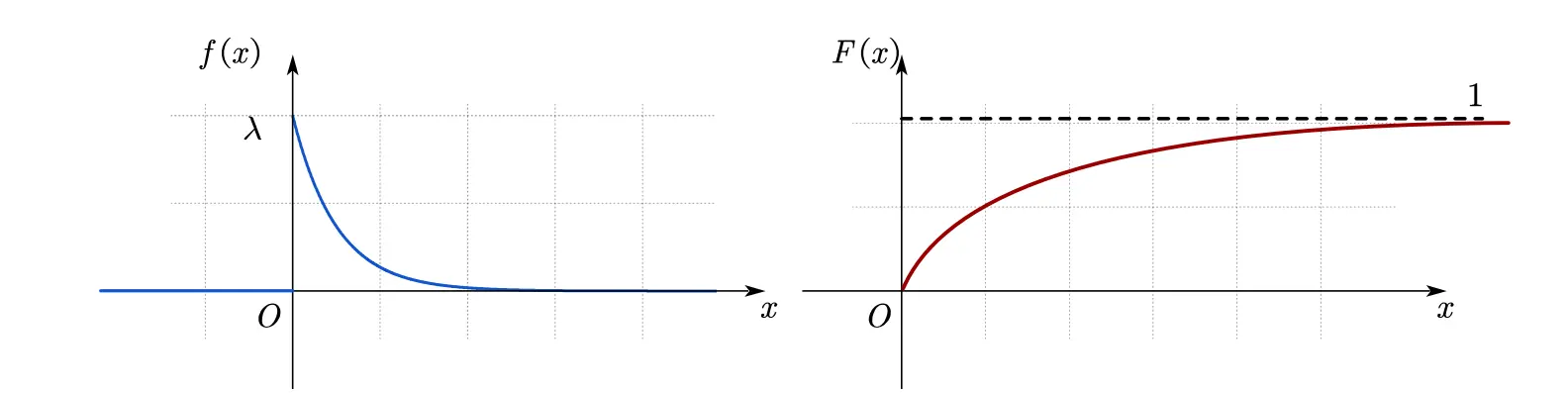
概率密度函数 (PDF)：

f(x)=\begin{cases} \lambda e^{-\lambda x}, & x\geq 0 \\ 0, & x<0 \end{cases}

概率分布函数 (CDF)：

F(x)=\begin{cases} 0, & x<0 \\ 1-e^{-\lambda x}, & x\geq 0 \end{cases}

期望：

\mu=\frac{1}{\lambda}

方差：

\sigma^2=\frac{1}{\lambda^2}

· 随机变量函数分布

(1). 离散型随机变量函数的分布

设随机变量 $X$ 的分布律为 $P\{X = x_k\} = p_k, k = 1, 2, \cdots$ ，则当 $Y = g(X)$ 的所有取值为 $y_j (j = 1, 2, \cdots)$ 时，随机变量 $Y$ 有分布律
$P\{Y = y_j\} = \sum_{g(x_k) = y_j} P\{X = x_k\}.$

(2). 连续型随机变量函数的分布

方法一：设随机变量 $X$ 的概率密度函数为 $f_X(x) \, (-\infty < x < +\infty)$ ，那么 $Y = g(X)$ 的分布函数为
$F_Y(y) = P\{Y \leq y\} = P\{g(X) \leq y\} = \int_{g(x) \leq y} f_X(x) dx,$
其概率密度为 $f_Y(y) = F_Y'(y)$ 。
方法二：设随机变量 $X$ 具有概率密度函数 $f_X(x) \, (-\infty < x < +\infty)$ ， $g(x)$ 为 $(-\infty, +\infty)$ 内严格单调的可导函数，则随机变量 $Y = g(X)$ 的概率密度为
$f_Y(y) = \left\{ \begin{array}{ll} [f_X(h(y))] |h'(y)|, & \alpha < y < \beta, \\ 0, & \text{others}, \end{array} \right.$
其中 $h(y)$ 是 $g(x)$ 的反函数，
$\alpha = \min\{g(-\infty), g(+\infty)\}, \beta = \max\{g(-\infty), g(+\infty)\}$

· 例题

设随机变量 $X$ 的概率密度函数如下：

f_X(x) = \begin{cases} \frac{x}{2}, & 0 \leq x \leq 2 \\ 0, & others \end{cases}

(1) $Y = 3X + 4$ 的概率密度函数。 (2) $Y = e^X$ 的概率密度函数。 (3) $Y = (X - 1)^2$ 的概率密度函数。

(1) 第一步：求 $Y$ 的分布函数
$F_Y(y) = P(Y \leq y) = P(3X + 4 \leq y) = P\left(X \leq \frac{y - 4}{3}\right) = F_X\left(\frac{y - 4}{3}\right)$
第二步：求 $Y$ 的概率密度函数
$f_Y(y) = \frac{\mathrm{d}F_Y(y)}{\mathrm{d}y} = \frac{\mathrm{d}F_X\left(\frac{y - 4}{3}\right)}{\mathrm{d}y} = f_X\left(\frac{y - 4}{3}\right) \cdot \frac{1}{3}$
第三步：代入 $f_X$ 中：
$f_Y(y) = \begin{cases} \frac{y - 4}{18}, & 4 \leq y \leq 10 \\ 0, & others \end{cases}$
(2) 第一步：求 $Y$ 的分布函数
$F_Y(y) = P(Y \leq y) = P(e^X \leq y) = P(X \leq \ln y) = F_X(\ln y)$
第二步：求 $Y$ 的概率密度函数
$f_Y(y) = \frac{\mathrm{d}F_Y(y)}{\mathrm{d}y} = \frac{\mathrm{d}F_X(\ln y)}{\mathrm{d}y} = f_X(\ln y) \cdot \frac{1}{y}$
第三步：代入 $f_X$ 中：
$f_Y(y) = \begin{cases} \frac{\ln y}{2y}, & 1 \leq y \leq e^2 \\ 0, & others \end{cases}$
(3) 第一步：求 $Y$ 的分布函数
$F_Y(y) = P(Y \leq y) = P((X - 1)^2 \leq y) = P\left[(1 - \sqrt{y}) \leq X \leq (1 + \sqrt{y})\right] = F_X(1 + \sqrt{y}) - F_X(1 - \sqrt{y})$
第二步：求 $Y$ 的概率密度函数
$f_Y(y) = \frac{\mathrm{d}F_Y(y)}{\mathrm{d}y} = f_X(1 + \sqrt{y}) \cdot \frac{1}{2\sqrt{y}} + f_X(1 - \sqrt{y}) \cdot \frac{1}{2\sqrt{y}}$
第三步：代入 $f_X$ 中：
$f_X(x) = \begin{cases} \frac{1}{2\sqrt{y}}, & 0 \leq y \leq 1 \\ 0, & others \end{cases}$

Part 3 二维随机变量

· 二维连续变量

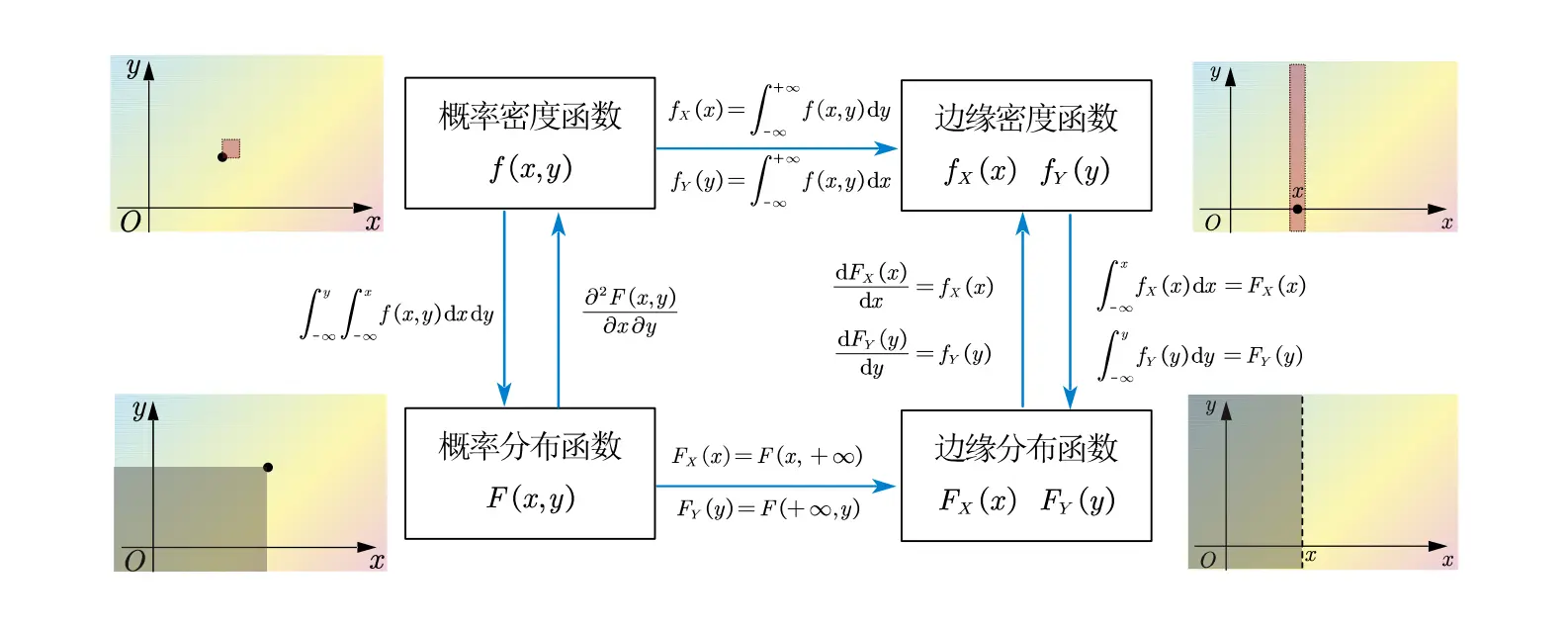
二维连续随机变量 $(X,Y)$ 的联合概率密度函数 $f(x,y)$ :

f(x, y) = \lim_{{\substack{\Delta x \to 0^+ \\ \Delta y \to 0^+}}} \frac{P(x \leq X \leq x + \Delta x, y \leq Y \leq y + \Delta y)}{\Delta x \cdot \Delta y}

二维连续随机变量 $(X,Y)$ 的联合概率分布函数 $F(x,y)$ :

F(x, y) = P\{X \leq x, Y \leq y\}

概率密度与概率分布之间的关系:

F(x, y) = \int_{-\infty}^{y} \int_{-\infty}^{x} f(u, v) du dv

f(x, y) = \frac{\partial^2 F(x, y)}{\partial x \partial y}

边缘概率密度函数 $f_X(x)$ 、 $f_Y(y)$ :

f_X(x) = \int_{-\infty}^{+\infty} f(x, y) dy\\ f_Y(y) = \int_{-\infty}^{+\infty} f(x, y) dx

边缘概率分布函数 $F_X(x)$ 、 $F_Y(y)$ :

F_X(x) = P\{X \leq x\} \\ F_Y(y) = P\{Y \leq y\}

彼此关联:

\frac{\mathrm{d}F_X(x)}{\mathrm{d}x} = f_X(x), \int_{-\infty}^{x} f_X(x) dx = F_X(x) \\ \frac{\mathrm{d}F_Y(y)}{\mathrm{d}y} = f_Y(y), \int_{-\infty}^{y} f_Y(y) dy = F_Y(y)

· 相互独立性

在二维随机变量 $(𝑋, 𝑌)$ 中，如果 $𝑋$ 和 $𝑌$ 相互独立，则有以下等式成立：

F{(x,y)}=F_X(x)\cdot F_Y(y)\\ f{(x,y)}=f_X(x)\cdot f_Y(y)

这两个式子也可以用来判断两个变量是否相互独立。

· 二维连续变量的函数

设 $(X,Y)$ 是二维连续随机变量，其联合概率密度为 $f(x,y)$ ，则随机变量 $Z$ 的常见函数形式包括：

和函数： $Z = X + Y$
商函数： $Z = \frac{Y}{X}$
积函数： $Z = XY$
最大值函数： $Z = \max\{X, Y\}$
最小值函数： $Z = \min\{X, Y\}$

对于上述任意函数形式，求 $Z$ 的概率分布函数 $F_Z(z)$ 或概率密度函数 $f_Z(z)$ 的步骤如下：

(1) 确定取值范围

根据 $(X,Y)$ 的联合分布范围，确定 $Z$ 的有效取值区间：

z \in [\alpha, \beta]

(2) 建立积分区域

在 $xOy$ 平面中，绘制不等式 $Z \leq z$ 对应的区域 $D$ ：

D = \left\{ (x,y) \mid g(x,y) \leq z \right\}

其中 $g(x,y)$ 表示 $Z$ 与 $(X,Y)$ 的函数关系式

(3) 计算分布函数

通过二重积分求概率：

F_Z(z) = P(Z \leq z) = \iint_D f(x,y) \,dx\,dy

(4) 求导得密度函数

对分布函数求导获得概率密度：

f_Z(z) = \frac{d}{dz} F_Z(z)

Part 4 随机变量的数字特征

· 期望方差

· 期望

/Definition/

(1). 离散随机变量
$E(X)=\sum_{i=1}^{n}X_{i}P(X=X_{i})$
(2). 一维连续随机变量
$E(X)=\int_{-\infty}^{+\infty}xf(x)dx$
(3). 二维连续随机变量
$E(X)=\iint_{-\infty}^{+\infty}xf(x,y)dxdy$ $E(Y)=\iint_{-\infty}^{+\infty}yf(x,y)dxdy$ $E\left(\frac{1}{XY}\right)=\iint_{-\infty}^{+\infty}\frac{f(x,y)}{xy}dxdy$

数学期望的性质:

(1). 线性性质

E(CX)=C\cdot E(X),\quad E(X+C)=E(X)+C \quad

(2). 可加性

E(X+Y)=E(X)+E(Y)

(3). 独立性：若 $X,Y$ 独立，则 $E(XY)=E(X)\cdot E(Y)$

· 方差

/Definition/

方差 $D$ ：衡量随机变量的分散程度
(1). 离散随机变量
$D(X)=\operatorname{Var}(X)=\sum_{k=1}^{\infty}[X_{k}-E(X)]^{2}P(X=X_{k})$
(2). 一维连续随机变量
$D(X)=\operatorname{Var}(X)=\int_{-\infty}^{+\infty}[x-E(X)]^{2}f(x)dx$

方差的性质:

(1). 线性变换

D(CX)=C^{2}D(X),\quad D(X+C)=D(X)

(2). 可加性

D(X+Y)=D(X)+D(Y)+2E\{[X-E(X)][Y-E(Y)]\}

若 $X,Y$ 独立，则 $D(X+Y)=D(X)+D(Y)$ .

(3). 简化计算

D(X)=E(X^{2})-[E(X)]^{2}

(4). 标准差

\sigma=\sqrt{D(X)}

分布	期望	方差
二项分布 $X \sim b(n, p)$	$np$	$np(1 - p)$
泊松分布 $X \sim \pi(\lambda)$	$\lambda$	$\lambda$
均匀分布 $X \sim U(a, b)$	$\frac{a + b}{2}$	$\frac{(b - a)^2}{12}$
正态分布 $X \sim N(\mu, \sigma^2)$	$\mu$	$\sigma^2$
指数分布 $X \sim Exp(\lambda)$	$\frac{1}{\lambda}$	$\frac{1}{\lambda^2}$

· 协方差

$E\{[X - E(X)][Y - E(Y)]\}$ 被称为随机变量 $X, Y$ 的协方差，记为 $\text{Cov}(c)$ 。

(1).

\text{Cov}(aX, bY) = ab \text{Cov}(X, Y)

其中 $a, b$ 是常数

(2).

\text{Cov}(X_1 + X_2, Y) = \text{Cov}(X_1, Y) + \text{Cov}(X_2, Y)

(3). 协方差的公式还可以等价于： $E(XY) - E(X)E(Y)$

基于协方差，还会产生一个概念：相关系数 $\rho_{xy}$

\rho_{xy} = \frac{\text{Cov}(X, Y)}{\sigma(X) \cdot \sigma(Y)} = \frac{E\{[X - E(X)][Y - E(Y)]\}}{\sqrt{D(X)} \sqrt{D(Y)}}

$\rho_{xy}$ 的取值介于 $[-1, 1]$ 之间，其越接近0说明两者线性相关性越低（ $\rho_{xy} = 0$ ，则称两变量不相关），绝对值越大则越呈线性相关（-1则是负相关，+1是正相关）。

注意：两变量不相关 $\neq$ 两变量独立，不相关不一定独立，但独立一定不相关。

· 随机变量的矩

一维随机变量的矩：对于一维随机变量 $X$ ：

k阶原点矩：
$E(X^{k}) \quad (k=1,2,\cdots)$
k阶中心矩：
$E[(X-EX)^{k}] \quad (k=2,3,\cdots)$

特殊情形：
数学期望 $EX$ 是 $X$ 的一阶原点矩
方差 $DX$ 是 $X$ 的二阶中心矩

二维随机变量的混合矩：设 $(X,Y)$ 是二维随机变量：

k+l阶混合原点矩：
$E(X^{k}Y^{l}) \quad (k,l=1,2,\cdots)$
k+l阶混合中心矩：
$E[(X-EX)^{k}(Y-EY)^{l}] \quad (k,l=1,2,\cdots)$

重要结论：协方差 $\text{Cov}(X,Y)$ 是 $X$ 与 $Y$ 的混合二阶中心矩。

Part 5 大数定理与中心极限定理

· 切比雪夫不等式

设随机变量 $X$ 的期望为 $E(X)$ ，方差为 $D(X)$ ，则对于任意给定的 $\epsilon > 0$ ，有：

P\{|X - E(X)| \geq \epsilon\} \leq \frac{D(X)}{\epsilon^{2}}

或等价地

P\{|X - E(X)| < \epsilon\} \geq 1 - \frac{D(X)}{\epsilon^{2}}

说明：
该不等式给出了随机变量偏离期望值的概率上界
方差 $D(X)$ 越小，偏离概率的上界越小
适用于任何具有有限方差的随机变量

· 大数定律

大数定理：在大量重复试验中，样本平均数会趋近于理论期望值。换句话说，当试验次数足够多时，实验结果的平均值会接近预期的长期平均值。

切比雪夫大数定律 (Chebyshev's LLN).
条件：
随机变量序列 $X_{1},X_{2},\cdots,X_{n},\cdots$ 相互独立
数学期望 $EX_{i}$ 和方差 $DX_{i}$ 都存在
方差有公共上界： $DX_{i}\leq c$ ( $i=1,2,\cdots$ )
结论：对任意 $\epsilon>0$ ，有
$\lim_{n\to\infty}P\left\{\left|\frac{1}{n}\sum_{i=1}^{n}X_{i}-\frac{1}{n}\sum_{i=1}^{n}EX_{i}\right|<\epsilon\right\}=1$
核心思想： "只要方差有限，大量重复试验的平均值会接近期望值"
伯努利大数定律 (Bernoulli's LLN).
条件：设 $X_{n}\sim B(n,p)$ ， $\mu_{n}$ 是 $n$ 次伯努利试验中事件 $A$ 发生的次数
结论：对任意 $\epsilon>0$ ，有
$\lim_{n\to\infty}P\left\{\left|\frac{\mu_{n}}{n}-p\right|<\epsilon\right\}=1$
核心思想： "投硬币这类事情，大量地实验结果里，频率会接近概率"
辛钦大数定律 (Khinchin's LLN).
条件：随机变量序列 $X_{1},X_{2},\cdots,X_{n},\cdots$ 相互独立同分布，且 $EX_{i}=\mu$
结论：对任意 $\epsilon>0$ ，有
$\lim_{n\to\infty}P\left\{\left|\frac{1}{n}\sum_{i=1}^{n}X_{i}-\mu\right|<\epsilon\right\}=1$
核心思想： "同一类型的随机变量，大量样本的平均值会接近期望值"