外观
数理统计
约 2291 字大约 8 分钟
2025-09-17
Part 1 数理统计基本概念
样本统计量定义:从总体中抽出n个独立同分布的个体 X1, X2, ⋯, Xn,记为样本(样本容量为n)。
样本均值:
Xˉ=n1i=1∑nXi
样本方差:
S2=n−11i=1∑n(Xi−Xˉ)2
样本标准差:
S=n−11i=1∑n(Xi−Xˉ)2
样本k阶原点矩:
Ak=n1i=1∑nXik,k=1,2,⋯
样本k阶中心矩:
Bk=n1i=1∑n(Xi−Xˉ)k,k=2,3,⋯
经验分布函数定义:设 X1, X2, ⋯, Xn 是来自总体X的一个样本,将样本观测值按从小到大的顺序排列为 x(1)≤x(2)≤⋯≤x(n)。经验分布函数 Fn(x) 定义为:
Fn(x)=⎩⎨⎧0,nk,1,x<x(1)x(k)≤x<x(k+1),k=1,2,⋯,n−1x≥x(n)
· 三大抽样分布
χ2 **卡方分布 (Chi-square Distribution) **
X=X12+X22+⋯+Xn2
条件要求:各分量 Xi∼N(0,1) 且相互独立,自由度为 n.
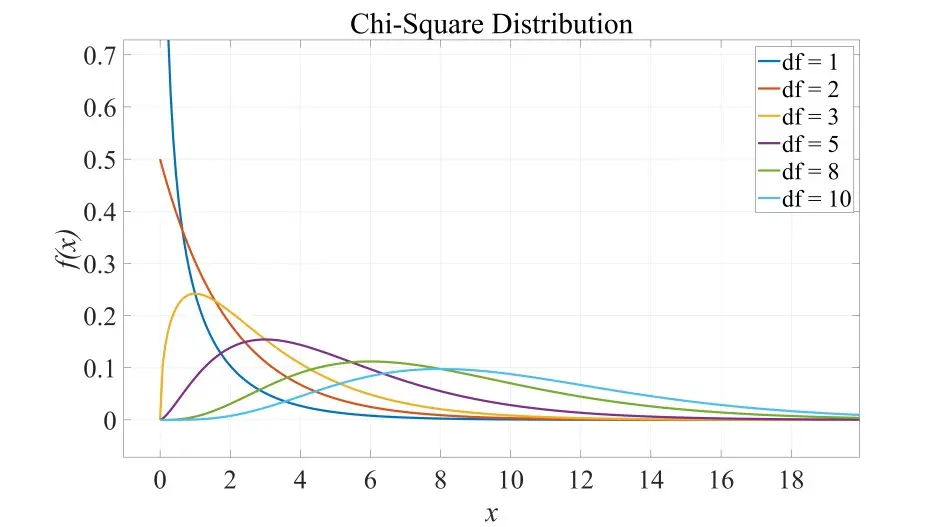
t分布 (Student's t-Distribution)
X=X2/nX1
条件要求:分子 X1∼N(0,1),分母 X2∼χ2(n),自由度为 n.
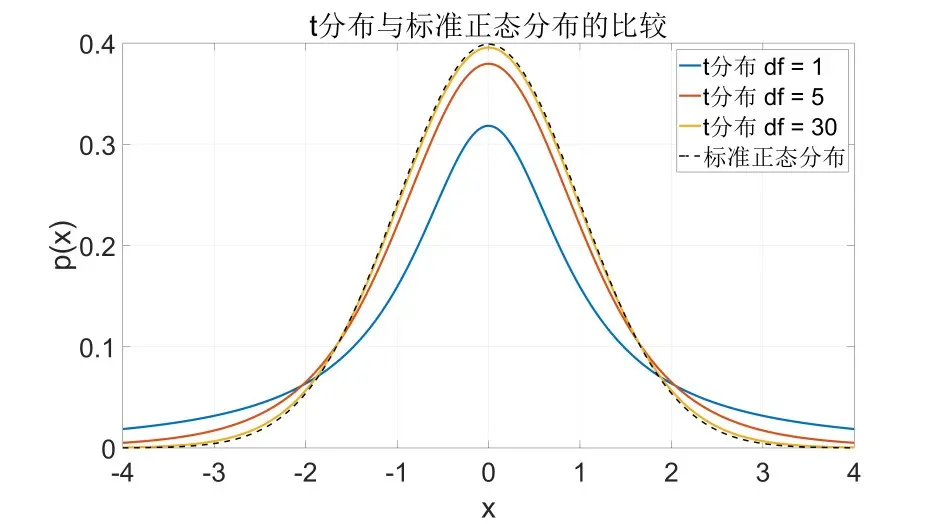
F分布 (F-Distribution)
X=X2/n2X1/n1
条件要求:分子 X1∼χ2(n1),分母 X2∼χ2(n2),自由度分别为 n1 和 n2.
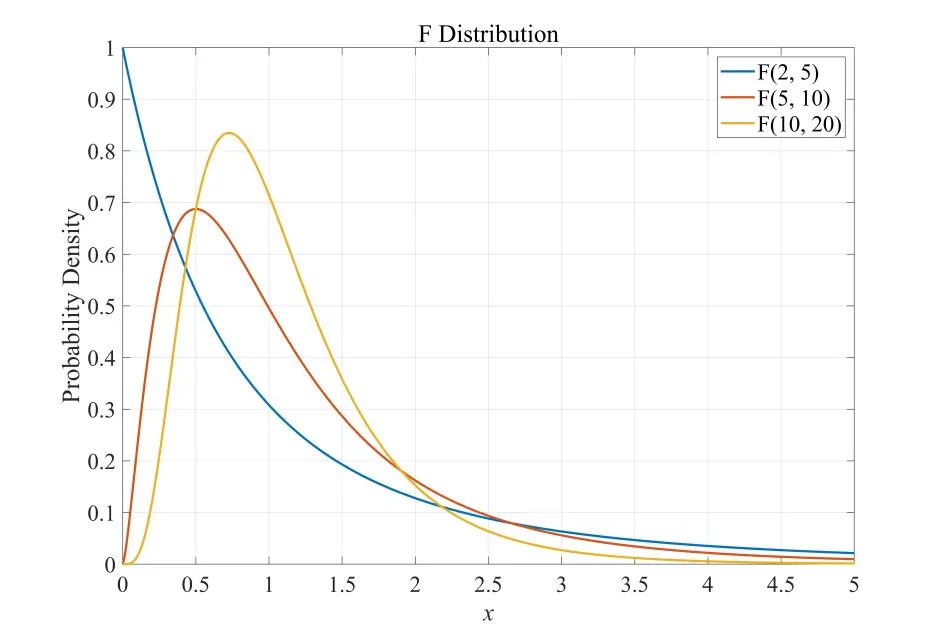
/Definition/
分位数定义:对于遵循某个分布的随机变量 X,给定一个参数 α(0<α<1),如果存在一个值X0满足:
P{X>X0}=α
则称 X0 为该分布的上 α 分位点。
不同分布的上 α 分位点表示
卡方分布:上 α 分位点记为 χα2(n).
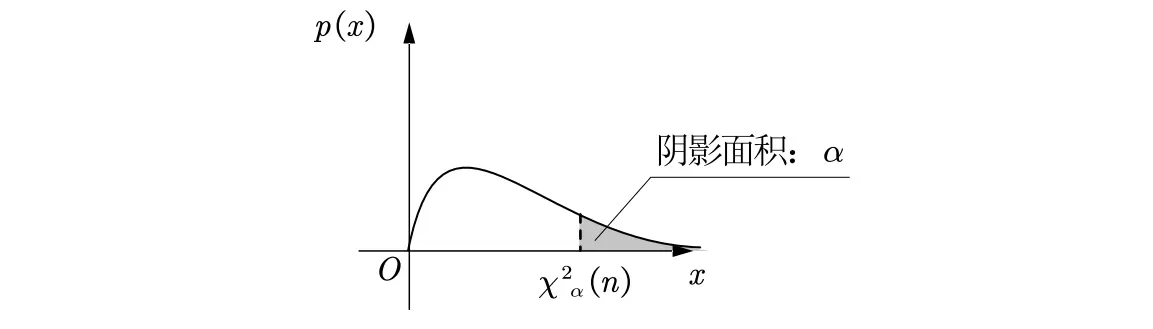
t分布:上 α 分位点记为 tα(n).
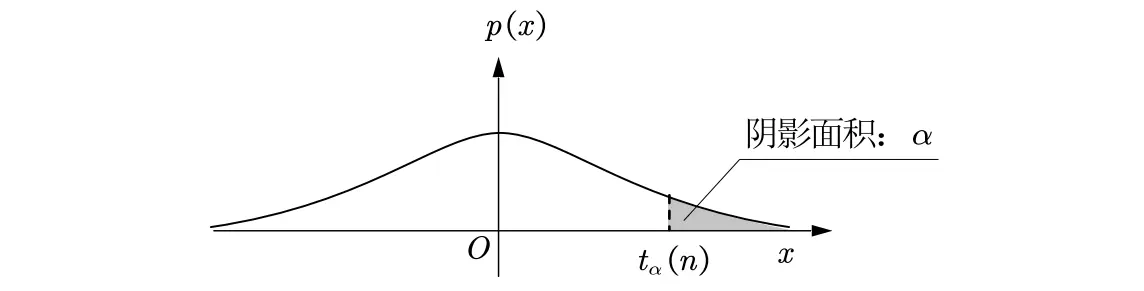
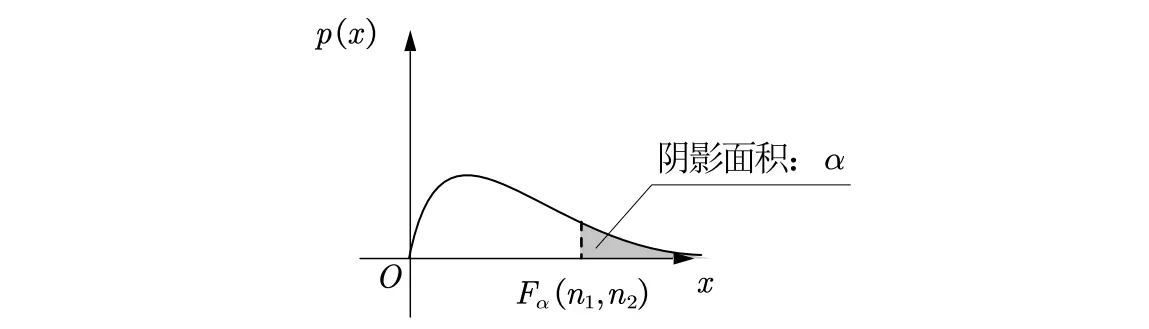
F分布:上 α 分位点记为 Fα(n1,n2).
· 样本均值与样本方差分布
单个正态总体
设总体 X∼N(μ,σ2),X1,X2,…,Xn 是来自总体 X 的简单随机样本,定义:
- 样本均值:
Xˉ=n1i=1∑nXi
- 样本方差:
S2=n−11i=1∑n(Xi−Xˉ)2
(1) 样本均值的分布
标准化样本均值(已知总体方差 σ2):
σ/nXˉ−μ=σn(Xˉ−μ)∼N(0,1)
t分布形式(未知总体方差,用样本方差 S2 替代):
S/nXˉ−μ=Sn(Xˉ−μ)∼t(n−1)
(2) 样本方差的分布
总体均值已知时:
σ21i=1∑n(Xi−μ)2∼χ2(n)
总体均值未知时(用样本均值 Xˉ 替代):
σ2(n−1)S2=i=1∑n(σXi−Xˉ)2∼χ2(n−1)
Part 2 参数估计与假设检验
我们需要用有限的样本数,来估算总体的状况。具体来说就是估计总体的实际平均值(有时候也估计总体的方差),而这里的“估计”又分为两类:
(1)估算实际平均值(例一);
(2)估算实际平均值会在哪个范围内(例二)。
前者我们称之为“点估计”,后者则是“区间估计”
· 点估计
矩估计:样本矩与总体矩相等。
第一步:如果要估计𝑛个参数,需要计算总体以及样本中的前𝑛阶原点矩;
第二步:样本矩=总体矩,得到𝑛个方程,可解出𝑛个参数的估计值;
最大似然估计:让参数取“最有可能”的值。
第一步:按照样本取值,写出对应“取得该值的概率”,即样本的似然函数;
第二步:令似然函数取得最大值,求得此时对应的参数值作为估计值。
· 习题
/example/ 设 X1,X2,⋯,Xn 为总体 X 的一个样本,求下列概率密度中未知参数 θ 的矩估计量和最大似然估计量。
概率密度函数:
f(x)={θ⋅2θx−(θ+1),0,x>2,others
其中 θ>1。
[矩估计].
计算总体期望:
μ=∫2∞xθ2θx−(θ+1)dx=θ−12θ
解得 θ 与 μ 的关系:
θ=μ−2μ
用样本均值 Xˉ 代替 μ,得到矩估计量:
θ^=Xˉ−2Xˉ
[最大似然估计].
构建似然函数:
L=(θ2θ)n(i=1∏nXi)−(θ+1)
取对数似然函数:
lnL=n(lnθ+θln2)−(θ+1)ln(i=1∏nXi)
对 θ 求导并令导数为零:
dθdlnL=n(θ1+ln2)−i=1∑nlnXi=0
解得最大似然估计量:
θ^=(n1∑i=1nlnXi−ln2)1
/example/
概率密度函数:
f(x)={θxθ−1,0,0≤x≤1,others
其中 θ>0。
[矩估计].
计算总体期望:
μ=∫01xθxθ−1dx=θ+1θ
解得 θ 与 μ 的关系:
θ=(1−μμ)2
用样本均值 Xˉ 代替 μ,得到矩估计量:
θ^=(1−XˉXˉ)2
[最大似然估计].
构建似然函数:
L=θn/2(i=1∏nXi)θ−1
取对数似然函数:
lnL=2nlnθ+(θ−1)i=1∑nlnXi
对 θ 求导并令导数为零:
dθdlnL=2θn+2θ1i=1∑nlnXi=0
解得最大似然估计量:
θ^=(∑i=1nlnXi)2n2
· 估计量的评选标准
设 θ 是总体 X 分布中的待估参数,其估计量为 θ^:
(1). 无偏性:若估计量的期望等于实际参数值,即:
E(θ^)=θ
则称 θ^ 是 θ 的无偏估计量。
(2). 有效性:对于同一参数 θ 的两个无偏估计量 θ^1 和 θ^2,若满足:
D(θ^1)<D(θ^2)
则称 θ^1 比 θ^2 更有效。
(方差越小,估计量越稳定,有效性越高)
(3). 一致性(相合性):当样本容量 n→∞ 时,若 θ^ 依概率收敛于 θ,即:
n→∞limP(∣θ^−θ∣<ε)=1(∀ε>0)
则称 θ^ 为 θ 的一致估计量。
· 区间估计
(1). 总体方差已知时(σ2已知):
σ/nXˉ−μ∼N(0,1)
(2). 总体方差未知时(σ2未知):
S/nXˉ−μ∼t(n−1)
(3). 总体方差分布:
σ2(n−1)S2∼χ2(n−1)
期望μ的置信区间
(1). σ2已知时,置信区间公式:
Xˉ±zα/2⋅nσ
(2). σ2未知时,置信区间公式:
Xˉ±tα/2,n−1⋅nS
符号说明:
- Xˉ:样本均值
- S:样本标准差
- n:样本数
- zα/2:标准正态分布的上α/2分位点
- tα/2,n−1:t分布(自由度n−1)的上α/2分位点
方差σ2的置信区间
置信区间公式:
(χ∗α/2,n−12(n−1)S2,χ∗1−α/2,n−12(n−1)S2)
符号说明:
- χα/2,n−12:χ2分布(自由度n−1)的上α/2分位点
- S2:样本方差
- n:样本数
· 假设检验
假设检验的类型与原理,与区间估计的几乎一致。但是以下概念需要清楚:
原假设和备择假设:称需要着重考察的假设为原假设,原假设常记为 H0;与原假设相对立的假设称为备择假设或对立假设,备择假设常记为 H1。
检验统计量:如果基于某一个统计量的观测值来确定接受 H0 或拒绝 H0 时,这一统计量称为检验统计量。
拒绝域和临界点:当检验统计量的观测值落在某个区域时就拒绝 H0,这一区域称为拒绝域,拒绝域的边界点称为临界点。
显著性水平 α:是一个小的正数,在作检验时要求犯第Ⅰ类错误的概率 ≤α,α 称为检验的显著性水平。α 通常取 0.1, 0.05, 0.01, 0.005 等值。
假设检验的两类错误:
- H0 实际上为真时,而拒绝 H0,这类弃真的错误称为第Ⅰ类错误。
- H0 实际上为假时,而接受 H0,这类取伪的错误称为第Ⅱ类错误。
显著性检验:对于给定的样本容量,只控制犯第Ⅰ类错误的概率,而不考虑犯第Ⅱ类错误的概率的检验法,称为显著性检验。
数理统计部分结束.
更新日志
2025/10/12 15:13
查看所有更新日志
c9ee8-plume于a28aa-a于
