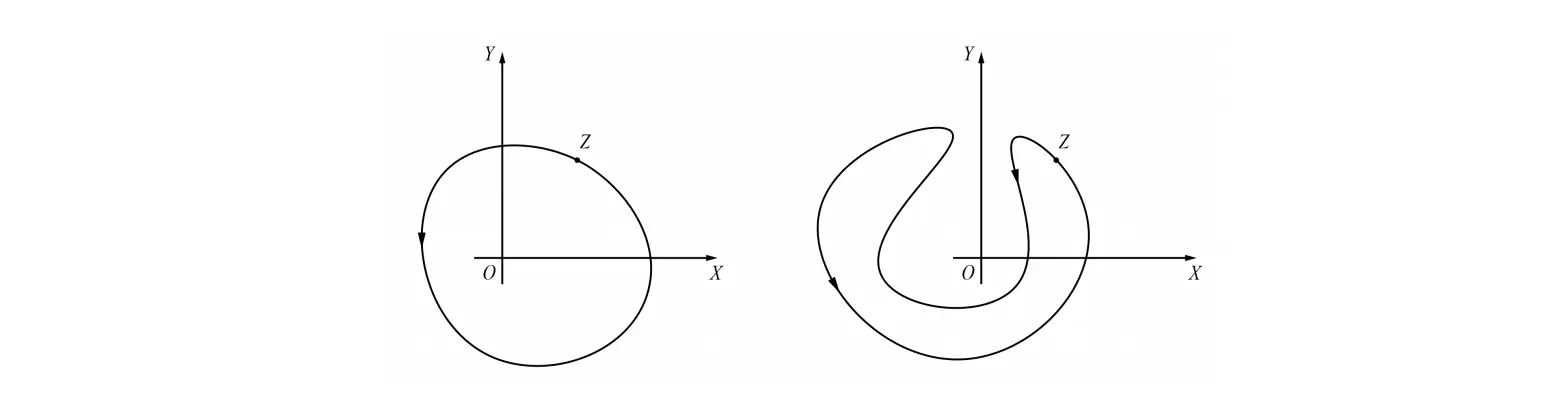Chapter 1 解析函数

复数当然包含实数，我们的目标是以复变量作为出发点，去研究它如何统治实变量的事实

——高木贞治《解析概论》

实际上复变函数和很多专业课的关联极强，四大力学的两门（电动力学和量子力学）都和古典数学物理有着很强的联系。“信号与系统”抑或“控制工程基础”这种专业课也离不开 ODE 以及 PDE 的大量存在，但解决这两个问题的前提便是复变函数。

在高木贞治的《解析概论》中更是使用一章的篇幅来讲述 “解析函数”，他本人将其视作“迅速掌握初等函数所必需的一项基本原则”。

当然，知乎上也有这样一段话：

复变函数论研究的是解析函数，而解析函数具有“刚性”，少量信息就能决定整体。

Fragment 1 复数

在中学课本中我们都学过如下的定义式：

$$i=\sqrt{-1}$$

· 定义

此时我们就可以尝试着定义复数和相关的概念：

/Definition/

• $z = x + iy$, $x, y \in \mathbb{R}$. 则 $z \in \mathbb{C}$. $\mathbb{C}$ 为复数集. $x$ 为 $z$ 的实部，记为 $\text{Re } z$. $y$ 为 $z$ 的虚部，记为 $\text{Im } z$. 则 $z = \text{Re } z + i \text{Im } z$.
• 复共轭：设 $z = x + iy$, 则 $\bar{z} = x - iy$ 称为其复共轭，又可以记为 $z^*$.
• 复数的模 $|z| = \rho = \sqrt{x^2 + y^2}$.

复平面上任意一点 $(x, y)$ 与复数 $z = x + iy$ 形成一一对应. 如果记点 $(x, y)$ 为 $P$, 则原点 $O$ 和 $P$ 一起可以构成向量 $\overrightarrow{OP}$, 称为复向量. 这三者有一一对应关系:

$$(x, y) \longleftrightarrow z = x + iy \longleftrightarrow \overrightarrow{OP}.$$

$(x, y)$ 可以用极坐标表示: $(\rho, \varphi)$. 其中模 $\rho \in [0, +\infty)$, 辐角 $\varphi \in (-\infty, +\infty)$. 因而有如下关系:

$$x = \rho \cos \varphi, \quad y = \rho \sin \varphi, \quad z = \rho (\cos \varphi + i \sin \varphi).$$

此为三角函数表示.

另外，我们还有指数表示形式 $z = \rho e^{i\varphi}$. 三种表示形式等价:

$$z = x + iy \longleftrightarrow z = \rho e^{i\varphi} \longleftrightarrow z = \rho (\cos \varphi + i \sin \varphi).$$

在复平面中，$x$ 轴称为实轴，$y$ 轴称为虚轴.

那这个时候我们要拿出谬论：

$$-1=\text{i}^2=\sqrt{-1}\cdot \sqrt{-1}=\sqrt{(-1)^2}=1$$

为什么？因为 $\sqrt{-1}$ 并非真正的代数运算。

引入复平面后，我们不难发现 $\text{i}$ 在乘上一个复数后能起到“旋转”的作用，那么，我们可以尝试使用线性空间来定义复数。

复数的矩阵定义：可以用 $2×2$ 方阵定义

$$a+b\text{i}\Rightarrow \begin{bmatrix} a & -b\\ b & a\\ \end{bmatrix}$$

Pauli 早在上个世纪就找到了这种对应.

因为是二维的线性空间，所以复数也能表示为一个矢量，加法满足平行四边形法则.

• $z\bar{z} = |z|^2 = x^2 + y^2$ ，显然这是一个单位圆

• $z$ 的辐角 $\varphi = \arg z \in (-\infty, +\infty)$. 辐角主值 $\operatorname{Arg} z \in (-\pi, +\pi]$, 也有的教材认为 $\operatorname{Arg} z \in [0, 2\pi]$. 则 $\varphi = \operatorname{Arg} z + 2k\pi$, $k \in \mathbb{Z}$.

复数的辐角有多值性：因为三角函数是周期性的，这是大多数复变函数困难的来源

复数乘法在极坐标表示下可以写成：

$$\alpha_1 \cdot \alpha_2 = r_1 r_2 [\cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2)]$$

(模相乘，辐角相加).

相对应的，除法是：

$$\frac{\alpha_1}{\alpha_2} = \frac{r_1}{r_2} [\cos(\theta_1 - \theta_2) + i \sin(\theta_1 - \theta_2)]$$

· 欧拉公式

/Theorem/

Euler 公式:

$$e^{i\theta} = \cos\theta + i\sin\theta$$

我们这里的写法是根据泰勒展开来定义 $e^{i\theta}$ 的. 我们已经知道，

$$e^x = \sum_{k=0}^{\infty} \frac{x^k}{k!}$$

Euler 认为这个式子在自变量为纯虚数时也成立，也就得到

$$e^{i\theta} = \sum_{n=0}^{\infty} \frac{(-1)^n \theta^{2n}}{(2n)!} + i \sum_{n=0}^{\infty} \frac{(-1)^n \theta^{2n+1}}{(2n+1)!}$$

/Theorem/

de Moivre公式（棣莫弗公式，由欧拉公式直接得到）：

$$(\cos \varphi + i \sin \varphi)^n = \cos n\varphi + i \sin n\varphi, \quad \Leftrightarrow \quad (e^{i\varphi})^n = e^{in\varphi}.$$

试着解决复数的开方：

设 $z = \rho e^{i\varphi}$。则

$$z^{\frac{1}{n}} = \rho^{\frac{1}{n}} e^{i\frac{\varphi + 2k\pi}{n}}, k = 0, 1, 2, \ldots, n-1.$$

将 $z^{\frac{1}{n}}$ 写成三角函数形式，并由三角函数的周期性易知，$k \geq n$ 之后，取值和 $k = 0, 1, \ldots, n-1$ 中的一个重复。

所以只有 $n$ 个不同方根。

Fragment 2 解析函数

复变函数是二维到二维的映射 ——TED

· 复变函数

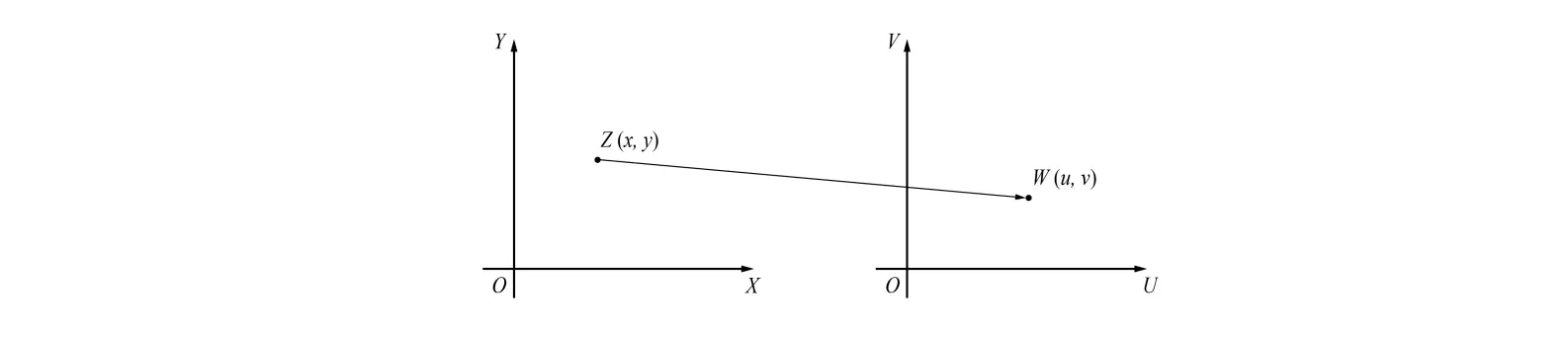
在定义复数的时候，笔者特意加入了一般教材没有的矩阵定义，以体现“二维到二维”的特点。复变函数可以看成是两个不同复平面上点集的对应关系，但这和以前的实变函数或者映射有所不同，因为对应关系可以是一一对应、多一对应甚至一多对应.

既然“复变函数可以看成是两个不同复平面上点集的对应关系”，我们可以先定义区域相关的概念.

/Definition/

邻域：$|z_0 - z| < \rho$ 定义为复平面上的一点 $z_0$ 的一个邻域（圆域），其中 $\rho > 0$ 为任意常数。有时会用去心邻域，这时要求 $0 < |z - z_0| < \rho$，但一般不会特别说明。

点集的内点：该点的一个邻域包含在点集当中。

区域（具有道路连通性的开集）：满足如下两个条件的点集。

1. 所有的点都是内点；
2. 有道路连通性。

简单的区域可以用不等式表示。

区域的边界点和边界：边界点不属于区域，但是其任意邻域中均有属于区域的点。边界点的全体称为边界。

闭区域：区域 $\cup$ 边界。

区域的边界方向：沿着边界走，区域保持在左方，则走向称为边界的正向。

/Definition/ (复变函数的一个不确切定义)

复平面上一个区域 $G$，如果对于每一个 $G$ 中的 $z$ 值，都有一个或多个复数值 $w$ 与之对应，则称 $w$ 为 $z$ 的函数——复变函数，记为 $w = f(z)$，定义域为 $G$。

暂时我们接受这个定义，但是显然这个定义有点问题，对应多个复数值显然不能叫做“函数”。

显然，$w = f(z) = u(x, y) + \mathrm{i}v(x, y)$。所以一个复变函数只不过是两个二元实变函数的有序组合。

正如微积分中研究函数一样，我们要研究复变函数的极限和连续性

复变函数的极限与连续:

$w = f(z)$ 在 $z_0$ 的某邻域有定义（在 $z_0$ 点不一定有定义），若 $\forall \varepsilon > 0$, $\exists \delta > 0$, 当 $0 < |z - z_0| < \delta$ 时，总有 $|f(z) - w_0| < \varepsilon$, 其中 $w_0$ 为一个确定的复数，则我们称 $w_0$ 为 $f(z)$ 在 $z_0$ 处的极限，记为

$\lim_{z \to z_0} f(z) = w_0.$

若 $f$ 在 $z_0$ 处有定义，且 $f(z_0) = w_0$，则称 $f$ 在 $z_0$ 处连续。

若 $f(z)$ 在 $\bar{\sigma} = \sigma + l$（闭区域）上连续，则

1. $f(z)$ 在 $\sigma$ 上有界。$\forall z \in \bar{\sigma}$, $\exists M \in [0, +\infty)$, $|f(z)| \leqslant M$。
2. 存在 $z_0 \in \bar{\sigma}$，使得 $|f(z_0)|$ 取最大/最小值。
3. 在闭区域 $\bar{\sigma}$ 上，$f(z)$ 一致连续。即对 $\forall \varepsilon > 0$, $\exists \delta > 0$, 它无关于 $z$, 对 $\bar{\sigma}$ 中满足 $0 < |z_1 - z_2| < \delta$ 的任意两点 $z_1, z_2$, 均有 $|f(z_1) - f(z_2)| < \varepsilon$。

· 解析函数

在数学分析里面我们常研究可微以及可导的概念，可以尝试将其推广到复变函数.

/Definition/

若 $f(z)$ 在 $z$ 及其邻域单值且连续，且极限

$$\lim_{\Delta z \to 0} \frac{f(z + \Delta z) - f(z)}{\Delta z}$$

在 $z$ 处存在、唯一、有限，并且与 $\Delta z \to 0$ 的方式无关，则称 $f(z)$ 在 $z$ 处可微，记为

$$f'(z) = \frac{\mathrm{d}f}{\mathrm{d}z} = \lim_{\Delta z \to 0} \frac{f(z + \Delta z) - f(z)}{\Delta z}.$$

因为复变函数的复杂性，我们一般会给出一个限制：解析

/Definition/

解析：$f(z)$ 在 $z_0$ 处及其某个邻域处处可导，则称 $f(z)$ 在 $z_0$ 处解析。

解析函数：$f(z)$ 在区域 $\sigma$ 上处处解析，则称 $f(z)$ 是区域 $\sigma$ 上的解析函数。

解析定义和微积分中“每一点都有无穷阶导数”的定义是等价的.

我们现在来研究可导的必要条件.

/Claim/

设函数 $f(z) = u + iv$ 在区域 $\sigma$ 解析。

记 $f(z + \Delta z) - f(z) = \Delta f = \Delta u + i\Delta v$，$ u = u(x, y)$，$v = v(x, y)$，$\Delta z = \Delta x + i\Delta y$。则

$$f'(z) = \lim_{\Delta z \to 0} \frac{\Delta f}{\Delta z} = \lim_{\Delta z \to 0} \frac{\Delta u + i\Delta v}{\Delta x + i\Delta y}.$$

由于 $\Delta z \to 0$ 的方式是任意的，因而我们可以让其通过两种不同方式趋近于 0：

1. 取 $\Delta z = \Delta x + i\Delta y = 0 + i\Delta y \to 0$，即令 $\Delta x = 0$，$\Delta y \to 0$：

   $$f'(z) = \lim_{\Delta x=0, \Delta y \to 0} \frac{\Delta u + i\Delta v}{\Delta x + i\Delta y} = \lim_{\Delta y \to 0} \frac{\Delta v}{\Delta y} - i \lim_{\Delta y \to 0} \frac{\Delta u}{\Delta y} = \frac{\partial v}{\partial y} - i \frac{\partial u}{\partial y}.$$

2. 取 $\Delta z = \Delta x + i\Delta y = \Delta x + i \cdot 0 \to 0$，即令 $\Delta x \to 0$，$\Delta y = 0$：

   $$f'(z) = \lim_{\Delta x \to 0, \Delta y=0} \frac{\Delta u + i\Delta v}{\Delta x + i\Delta y} = \lim_{\Delta x \to 0} \frac{\Delta u}{\Delta x} + i \lim_{\Delta y \to 0} \frac{\Delta v}{\Delta x} = \frac{\partial u}{\partial x} + i \frac{\partial v}{\partial x}.$$

由于导数具有唯一性，我们可以得出必要条件：

/Theorem/ (Cauchy - Riemann 条件)

$$\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} \quad \quad \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}.$$

· 解析函数判定定理

/Theorem/

若 $f(z) = u + iv$ 在区域 $\sigma$ 上满足：

1. $C-R$ 条件；
2. $u(x, y), v(x, y)$ 存在连续的一阶偏导数，

那么可以判断 $f(z)$ 在区域 $\sigma$ 上是解析的。

我们已经证明了C-R条件，那接下来需要证明的就是条件2

/proof/

记 $\frac{\partial u}{\partial x} = u_x$，$\frac{\partial u}{\partial y} = u_y$，$\frac{\partial v}{\partial x} = v_x$，$\frac{\partial v}{\partial y} = v_y$。由于这些偏导都存在且连续，因而 $u, v$ 存在全微分

$$du = u_x dx + u_y dy, \quad dv = v_x dx + v_y dy,$$

代入 $df = du + i dv$，得

$$df = (u_x + i v_x) dx + (v_y - i u_y) idy.$$

由 $C-R$ 条件，有 $u_x = v_y$，$v_x = -u_y$，故

$$df = (u_x - i u_y) dx + (u_x - i u_y) idy.$$

提公因子，并利用 $dz = dx + i dy$，得

$$df = (u_x - i u_y) dz.$$

故有 $\frac{df}{dz} = u_x - i u_y$，$f(z)$ 在区域 $\sigma$ 处处可导。因此在区域 $\sigma$ 上处处解析，所以 $f(z) = u + iv$ 在区域 $\sigma$ 上是解析函数，且有

$$\frac{df}{dz} = \frac{\partial u}{\partial x} - i \frac{\partial u}{\partial y}.$$

我们先对所用符号进行一些补充说明。

式中 $\nabla^2$ 为 Laplace 算符（拉普拉斯算符）：

$$\nabla^2 \equiv \nabla \cdot \nabla.$$

其中梯度算符 $\nabla$ 和维数有关，最常见的是二维和三维的形式：

$$\nabla = \left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y} \right) \quad \text{or} \quad \nabla = \left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z} \right).$$

二维拉普拉斯算符，记为 $\nabla_2^2 = \Delta_2$，则

$$\nabla_2^2 = \nabla_2 \cdot \nabla_2 = \left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y} \right) \left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y} \right) = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}$$

同理三维的拉普拉斯算符 $\nabla_3^2 = \Delta_3 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}$，其对应的拉普拉斯方程形式为

$$\nabla_3^2 u(x, y, z) = 0.$$

其中 $u$ 是任意函数。形如 $\nabla^2 u = 0$ 的方程称为拉普拉斯方程。若方程的形式是 $\nabla^2 u = f$，则称这类方程为 Poisson 方程（泊松方程）。显然，前者是后者的特例。（注意，这里的 $u$, $f$ 和一开始设的 $f(z) = u + iv$ 中的 $u$, $f$ 含义不同。在说明泊松方程时设的 $u$, $f$ 均是任意函数。）

在不产生歧义的前提下，可以直接将拉普拉斯算符的下标（例如 2 或 3，分别表示二维和三维的拉普拉斯算符）省略，只写成 $\nabla^2$.

若 $f(z) = u + iv$ 在区域 $\sigma$ 上是解析函数，则有如下两个结论：

(1). $ u(x, y) $ 与 $ v(x, y) $ 是 $ \sigma $ 上的调和函数，也即：

$$\begin{cases} \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = \nabla^2 u(x, y) = 0, \\ \frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} = \nabla^2 v(x, y) = 0. \end{cases}$$

/proof/

证明：因为 $f(z)$ 是区域 $\sigma$ 上的解析函数，所以 $f(z) = u + iv$ 满足 $C-R$ 条件：

$$\begin{cases} \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, & 1' \\ \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}. & 2' \end{cases}$$

$1'$ 式两边对 $x$ 求偏导，得

$$\frac{\partial^2 u}{\partial x^2} = \frac{\partial^2 v}{\partial x \partial y}.$$

$2'$ 式两边对 $y$ 求偏导，得

$$\frac{\partial^2 u}{\partial y^2} = -\frac{\partial^2 v}{\partial y \partial x}.$$

以上两式相加，得

$$\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = \frac{\partial^2 v}{\partial x \partial y} - \frac{\partial^2 v}{\partial y \partial x} = 0.$$

同理可证，$\frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} = 0$。因此 $u, v$ 均是调和函数。

事实上，后面的柯西积分公式会说明解析函数的任意阶导数存在，因而 $f(z)$ 的任意阶导数都是连续的. 由于关于 $z$ 连续就意味着关于 $x$ 和 $y$ 均连续，故容易由此证明 $v$ 的二阶混合偏导均连续

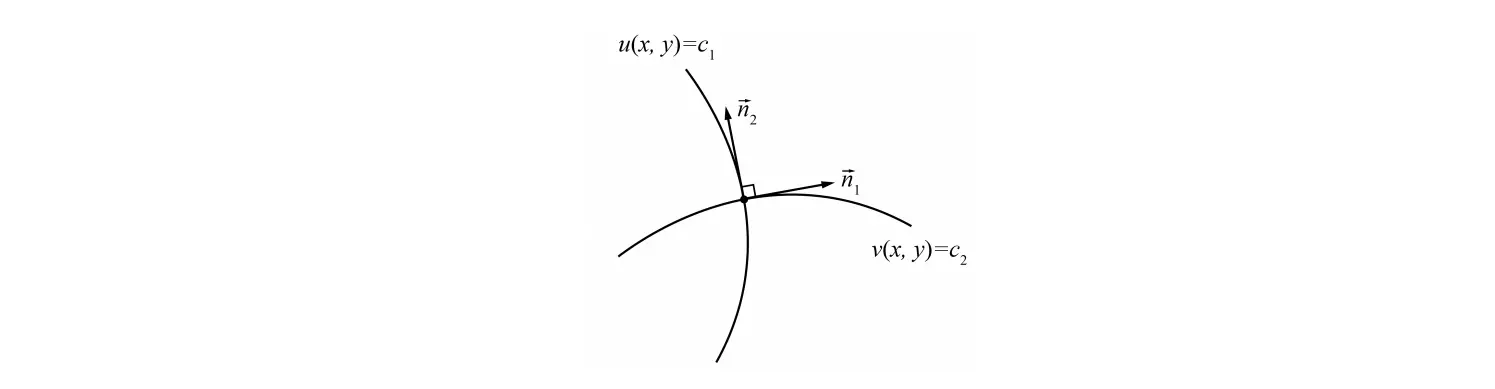
(2). $u$ 的等值线方程 $u(x, y) = c_1$ 与 $v$ 的等值线 $v(x, y) = c_2$ 在相交处相互正交。

/proof/

$u, v$ 的梯度为

$$\nabla u = \left( \frac{\partial u}{\partial x}, \frac{\partial u}{\partial y} \right), \quad \nabla v = \left( \frac{\partial v}{\partial x}, \frac{\partial v}{\partial y} \right).$$

利用 $C-R$ 条件，有

$$\nabla u \cdot \nabla v = \frac{\partial u}{\partial x} \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y} \frac{\partial v}{\partial y} = \frac{\partial u}{\partial x} \frac{\partial v}{\partial x} + \left( -\frac{\partial v}{\partial x} \right) \left( \frac{\partial u}{\partial x} \right) = 0.$$

注意梯度 $\nabla u$，$\nabla v$ 分别代表 $u$，$v$ 等值线上一点的法线方向，因此由上式知法线相互垂直，因而 $u$ 的等值线方程 $u(x, y) = c_1$ 与 $v$ 的等值线 $v(x, y) = c_2$ 在相交处相互正交。

因为 Cauchy - Riemann 条件的限制，解析函数的实部和虚部不是相互独立的. 比如从一个 $u(x,y)$ (实部) 确定虚部.

$$\int^{(x,y)} \left[ -\frac{\partial u}{\partial y} \, dx + \frac{\partial u}{\partial x} \, dy \right]$$

· 初等解析函数

(1). 指数为整数的幂函数：

$$w(z) = z^n, \quad n \in \mathbb{Z}.$$

若 $n \geq 0$，则 $w = z^n$ 在整个复平面上处处解析；

若 $n < 0$，则 $w = z^n$ 除 $z = 0$ 外在复平面上处处解析。

注意：“整个复平面”一般不含无穷远点，含无穷远点的叫扩充复平面。事实上我们可以证明在扩充复平面上全平面解析的函数只能是常函数

(2). 指数函数：

$$w(z) = e^z.$$

由于我们承认如下定义

$$e^x \equiv \sum_{k=0}^{\infty} \frac{1}{k!} x^k, \quad x \in \mathbb{R},$$

我们将这个定义推广到复数域，认为在复数域上式仍成立，那么根据正弦、余弦函数的泰勒展开式，可得

$$e^{ix} = \cos x + i \sin x,$$

因而

$$e^z = e^{x+iy} = e^x (\cos y + i \sin y).$$

也可以反过来从最后一个式子出发，认为最后一个式子是 $e^z$ 扩充到复数域后的定义（即 $e^z$ 的定义），验证前两个式子在实数域成立，以说明这样的定义是合法的。

具有周期性，周期为 $2\pi i$.

(3). 三角函数：$\sin z\,,\cos z$.

定义

$$\begin{cases} \sin z \equiv \frac{e^{iz} - e^{-iz}}{2i}, \\ \cos z \equiv \frac{e^{iz} + e^{-iz}}{2}. \end{cases}$$

其中，$z = x + iy \in \mathbb{C}$。

在这种情况下，

1. 它们的函数值可以大于1（例如取 $z = i$，则 $\cos i = \frac{e^{-1} + e^1}{2} > 1$，在值域上与实数很不相同）；

2. $$\sin^2 z + \cos^2 z = 1,\quad \quad \tan^2 z + 1 = \sec^2 z$$

3. $$\sin(z_1 + z_2) = \sin z_1 \cos z_2 + \cos z_1 \sin z_2 ,\quad\quad \cos(z_1 + z_2) = \cos z_1 \cos z_2 - \sin z_1 \sin z_2.$$

4. $$(\cos z)' = -\sin z ,\quad (\sin z)' = \cos z$$

5. $$\tan z \equiv \frac{\sin z}{\cos z} (\cos z \neq 0) \quad\quad \cot z \equiv \frac{\cos z}{\sin z} (\sin z \neq 0) \\ \sec z \equiv \frac{1}{\cos z} (\cos z \neq 0) \quad\quad \csc z \equiv \frac{1}{\sin z} (\sin z \neq 0)$$

(4). 双曲函数：$\sinh z, \cosh z$.

也通过复指数函数定义：

$$\sinh z = \frac{e^z - e^{-z}}{2}, \quad \cosh z = \frac{e^z + e^{-z}}{2}$$

简单的关系就是 $i \sinh(iz) = \sin z, \cosh(iz) = \cos z$.

· 多值函数

辐角本身的旋转引起了函数最后的多值性，但辐角主值不变 ——TED

在多值函数开始前先给出概念：

/Definition/

对于多值函数而言， 存在某些特殊点， 变量绕它转一圈回到原处之后对应的函数值没有还原， 这样的点称为该多值函数的支点，

(1). 根值函数

$$w(z) = \sqrt[n]{z}, \quad z \in \mathbb{C}, n \in \mathbb{N}, n \geq 2.$$

我们先以 $w(z) = \sqrt{z}$ 为例说明根式函数。它是一个多值函数。设 $w(z) = \rho e^{i\varphi}, z = re^{i\theta}$，则有

$$\rho^2 e^{2i\varphi} = z = re^{i\theta} = re^{i(\theta + 2k\pi)}, \quad k \in \mathbb{Z}$$

$$\Rightarrow \rho = \sqrt{r}, 2\varphi = \theta + 2k\pi, \quad k = 0, 1$$

$$\Rightarrow \varphi_1 = \frac{\theta}{2}, \varphi_2 = \frac{\theta}{2} + \pi$$

$$\Rightarrow w(z) = \begin{cases} \sqrt{r}e^{i\frac{\theta}{2}}, \\ -\sqrt{r}e^{i\frac{\theta}{2}}. \end{cases}$$

这说明 $w(z)$ 有两个独立的支。在复平面上，此时我们称原点 $O$ 是 $ \sqrt{z} $ 的支点：

若 $z$ 所对应的点 $Z$ 一开始与 $w_1 = \sqrt{r}e^{i\frac{\theta}{2}}$ 相对应，让 $Z$ 运动一周回到原来的地方，且运动轨迹把支点 $O$ 包围了起来（如下左图），那么它的函数值将从一个支跳到另一个支上，这是因为辐角从 $\theta$ 变成了 $\theta + 2\pi$，开方后辐角一个是 $\frac{\theta}{2}$ （对应结果 $\sqrt{r}e^{i\frac{\theta}{2}}$），一个是 $\frac{\theta}{2} + \pi$ （对应结果 $-\sqrt{r}e^{i\frac{\theta}{2}}$）；如果运动一周的轨迹并没有把支点包围（如下右图），其辐角仍为 $\theta$，即辐角前后不变，则不会跳到另一个支上。

多值函数因其多值性，不是可导的，因而不是解析的。为了实现根式函数的可解析化（以便利用解析函数的性质），我们需要其函数值和自变量一一对应的关系，一个自然的想法就是把这个多值函数分割成多个单值函数，这需要人为去定义支割线的概念。

下面我们用支割线定义单值的解析函数。

仍以 $w(z) = \sqrt{z}$ 为例。注意到 $z=0, \infty$ 均是 $w(z) = \sqrt{z}$ 的支点，连接两个支点形成一条射线（例如 $x$ 正半轴或负半轴），这条线就是一条支割线。若 $ z $ 在连续轨迹上运动没有越过支割线而回到原来位置，那么我们认为它始终在原来的支上运动。只要能够始终在同一个支上运动，就有我们所需要的一一对应的关系，此时函数就是单值的。

如果跨越了支割线一次，就跨越到另一个支上。跨越后，轨迹上的某一点 $P'$ 的辐角，相较于跨越前复平面上同一点 $P$ 的辐角，增加了 $2\pi$。（这里 $P$ 与 $ P’ $ 重合，只是后者辐角增加了 $2\pi$，这是跨越支割线的结果。如果轨迹没有跨过支割线而回到 $P$ 点，记为 $ P’’ $，则 $ P’’ $ 的辐角和 $ P $ 相同。）

另外，由以上可以看出，作支割线的方法不是唯一的。

关于 $z=\infty$ 是 $w(z) = \sqrt{z}$ 的支点，可借助黎曼球思考，无穷远点在黎曼球上相当于最上面的点，那么判定支点依据的“画半径任意小的圆”在针对无穷远点的情况时，就变成了在复平面上以原点为圆心、半径任意大圆的圆。因为只有这样的圆，才对应黎曼球上以无穷远点为圆心、半径任意小的圆，因而我们很容易能够推出“绕有限远处所有支点一圈”是黎曼球上以无穷远点为圆心“半径足够小”的结果。

我们很容易证明，“绕有限远处所有支点一圈回到原来的点时，函数值不能恢复”是“无穷远点为支点”的充要条件。因而，判断无穷远点是否为支点的方法就是，对包围有限远处所有的支点的轨迹进行讨论，看函数值绕一圈后是否恢复。

若无特殊指明，均认为所考虑的函数是单值函数.

· 黎曼面

在多值函数中，由于是一对多的对应，所以严格意义上讲，应该是一张复平面上的点对应多张复平面的同一位置的点，这多张复平面中每张代表代表一个支. 我们也可以避免画多张复平面的做法，把一对多的结果全部画在同一张图里面，这就需要采用黎曼面. 黎曼面将不同的支连接起来，形成一个有复杂拓扑结构的曲面.

实际上，多值函数并不定义在复平面上，而是定义在 Riemann 曲面上，在这个曲面上，多值函数不再成为多值函数，而是一个单值的多复变函数. 但是我们并不会使用 Riemann 曲面来做复变函数的问题，因为太过于困难.

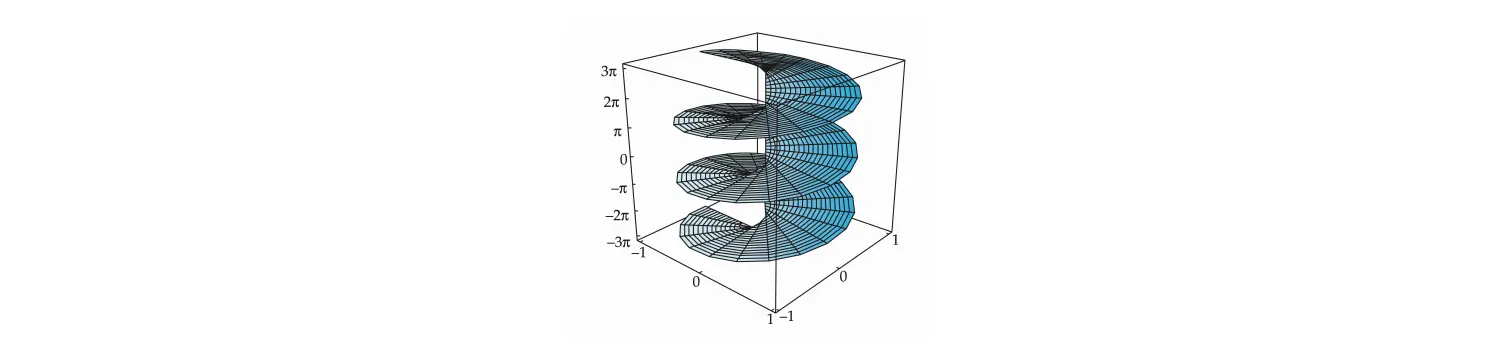
黎曼面的具体连接方法，是将所有支沿支割线剪开，然后将上一个支的下缘和下一个支的上缘连接起来，形成的三维立体结构，$x$ ; $y$两个方向代表原来复平面的两个方向，$z$ 轴代表辐角大小. 以 $G(z) = \arg z$ 为例，它有无穷多个支，其黎曼面如下：

(2). 对数函数：多值的对数函数 $w(z) = \ln z$ 定义为

$$\ln z \equiv \ln |z| + i \arg z,$$

设 $z = r e^{i\theta}$. 则

$$\ln z = \ln r + i(\theta + 2k\pi), \quad k=0, \pm1, \pm2, \ldots$$

$\ln z$ 称为复对数 (complex logarithm).

由 $k$ 的取值情况，可知 $\ln z$ 有无穷多个支. 由于 $\ln z = \ln (z - 0)$，所以容易判断原点为有限远处唯一支点，绕原点一圈相当于绕无穷远点一圈，所以无穷远点也是支点. 连接原点和无穷远点形成支割线（从原点 $O$ 指向无穷远点，例如正半实轴或负半实轴）.

若取正半实轴为支割线，对于辐角范围是 $(2k\pi, 2(k+1)\pi]$ 的某个支，上缘辐角是 $2k\pi$，下缘辐角为 $2(k+1)\pi$. 其中，上缘辐角指的是该支的辐角起点，下缘辐角是支的辐角终点.

从几何上看，上缘辐角是复平面上一个点从正半实轴上方不断趋近但不跨越正半实轴时辐角的极限，下缘辐角是复平面上一个点从正半实轴下方不断趋近但不跨越正半实轴时辐角的极限.

另外，由 $z = r e^{i\theta}$，知

$$e^{\ln z} = e^{\ln r + i(\theta + 2k\pi)} = e^{\ln r} e^{i(\theta + 2k\pi)} = r e^{i\theta} = z$$

即以下等式恒成立:

$$z = e^{\ln z}.$$

单值的对数函数 $w(z) = \operatorname{Ln} z$ 定义为

$$\operatorname{Ln} z \equiv \ln |z| + i \operatorname{Arg} z,$$

$\operatorname{Ln} z$ 称为复对数主值（the principal value of the complex logarithm），它是 $\ln z$ 对应的辐角属于 $(-\pi, \pi]$ 的情况，又称为主值支.

(3). 一般指数函数：

$$w(z) = a^z, \quad a, z \in \mathbb{C}, \quad a \neq 0.$$

其中，利用 $a = e^{\ln a}$，得

$$a^z = e^{z \ln a}.$$

显然，一般指数函数为多值函数。

(4). 一般幂函数：

$$w(z) = z^s, \quad s = a + ib \in \mathbb{C},$$

其中，利用 $z = e^{\ln z}$，可得

$$z^s = e^{s \ln z}.$$

而在下一章的复变积分中，我们将看到复变函数最优美的一些性质.