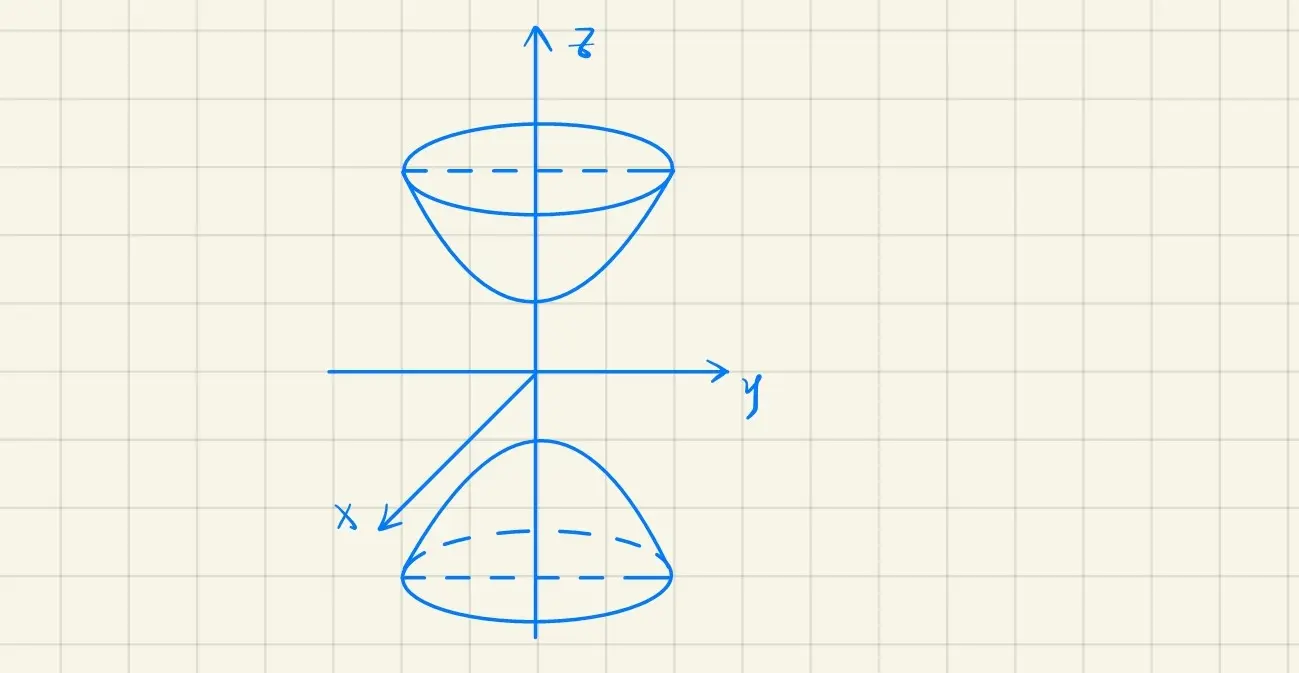Fragment 1 向量
· 向量基本运算
1.以量度或不变来分:变量与常量
2.以量的特征来分:
(1) 只有大小的量称为数量,或称为标量,或称为纯量
(2) 不仅有大小,而且还有方向称向量,或称为向量,常用 a, b, c 表示
而 ∣a∣, ∣b∣, ∣c∣ 表示矢量的大小,称为模长;有时也用 AB 表示,模长 ∣AB∣=AB
定义:若 a, b 大小相等,方向一致,称 a=b
大小 ∣ma∣=∣m∣∣a∣
性质:
(mn)a=m(na)=(nm)a(n+m)a=na+ma
· 向量加减
/property/
交换律:
a+b=b+a
结合律:
a+b+c=a+(b+c)=(a+b)+c
· 数量积
/example/ 一个质点M在恒力下的作用下,沿直线从A点移动到B点所做的功W
W=∣F∣⋅cosθ⋅∣AB∣=∣F∣∣AB∣cosθ=F⋅AB
/Define/
定义:设 a, b 为两个向量
定义两向量 a, b 的夹角 θ (0≤θ≤π)
a⋅b=∣a∣∣b∣cosθ
称为两向量 a 与 b 的点乘积,或点积,或数量积,或内积
然后给出性质:
/property/
性质1:
a⋅b=b⋅a
性质2:
a⋅(b+c)=a⋅b+a⋅c
性质3:
a⊥b⟺a⋅b=0
反之,若 a⋅b=0
⇒∣a∣∣b∣cosθ=0
⇒cosθ=0 或 ∣a∣=0 或 ∣b∣=0
⇒θ=2π, 即 a⊥b
或 ∣a∣=0⇒a=0
写成 a=0
性质4:
a⋅a=∣a∣∣a∣cos0=∣a∣2∣a∣=a⋅a
/example/ 设 a, b, c 两两互相垂直,
∣a∣=1,∣b∣=2,∣c∣=3
求 ∣a+b+c∣
/proof/
∣a+b+c∣=(a+b+c)⋅(a+b+c)
=a⋅a+b⋅b+c⋅c=12+22+32=14
点乘积的物理意义:一个质点M在恒力F的作用下沿直线由A点移动到B点所做的功W = F⋅AB
/Define/
设 a=0,即 ∣a∣=0,
称 ∣a∣a 为 a 的单位矢量,记作 a^,即 a^=∣a∣a
⇒a=∣a∣a^∣a^∣=∣a∣a=∣a∣1∣a∣=1
a^ 是单位矢量,求矢量 a 在非零矢量 b 上的投影:
Prjb⋅a=OP=∣a∣cosθ=∣a∣b^cosθ=a⋅b^=a⋅∣b∣b=∣b∣a⋅b
投影矢量 OP=OPb^
=(a⋅b^)b^
· 向量叉乘
我们引入一个开门的模型:
门径里开往处开大小定义为 ∣F∣∣AB∣sinθ,方向与 F,AB 确定的平面垂直
且 n, m 与方向构成右手系 (符合右手法则),这个矢量记为 F×AB
/Define/
设 a, b 为任意向量
定义一个新的向量 a×b :∣a×b∣=∣a∣∣b∣sinθ
a×b 的方向如下确定:a×b 与 a ,b 确定的平面垂直 ,且 a , b , a×b 构成右手系
称为 a 与 b 的叉乘积,或叉积,或矢量积,或外积
性质如下:
/property/
-
a×b=−b×a
-
a×(b+c)=a×b+a×c
-
a∥b⇔a×b=0
若 a∥b⇔a, b 线性相关, 存在不全为 0 的常数 k1, k2, 使 k1a+k2b=0
不妨设 k1=0, 有 a=−k1k2b ,令 −k1k2=λ, 有 a=λb
- (a⋅b)2+∣a×b∣2=∣a∣2∣b∣2
PS:点乘可为负,叉乘必非负
然后补充了一条数量级的性质(高中知识)
a⋅b=∣a∣∣b∣cosθ(0≤θ≤π)
当 a=0, b=0 时,
cosθ=∣a∣∣b∣a⋅b
· 空间直角坐标
· 集合直积
/example/ A={0,1}, B={1,2}
定义 A 与 B 的直积A×B={(0,1),(0,2),(1,1),(1,2)} , A×A=A2
设 R=(−∞,+∞),R×R=R2={(x,y)∣x,y∈R}
二维平面: R×R×R=R3={(x,y,z)∣x,y,z∈R}
三维空间: n个R×R×⋯×R=Rn
Rn={(x1,x2,…,xn)∣x1,x2,…,xn∈R}
n>3 时,称为抽象空间
· 空间直角坐标系
全体空间点组成的集合与 {(x,y,z)∣x,y,z∈R}=R3 建立一一对应。
三个平面把空间分成八个卦限
第一卦限:x>0, y>0, z>0
xOy 平面方程:z=0 , yOz 平面方程:x=0 , zOx 平面方程:y=0
x 轴方程:{y=0z=0 , y 轴方程:{x=0z=0 , z 轴方程:{x=0y=0
M(x,y,z) 关于 xOy 平面对称点为 (x,y,−z)
oz 轴对称点为 (−x,−y,z) , O 点对称点为 (−x,−y,−z)
· 空间两点间距离
设 P1(x1,y1,z1), P2(x2,y2,z2)∈R3
∣P1P2∣=(x2−x1)2+(y2−y1)2+(z2−z1)2
设 P1(x1,x2,x3,x4), P2(y1,y2,y3,y4)∈R4
∣P1P2∣=(y1−x1)2+(y2−x2)2+(y3−x3)2+(y4−x4)2
设 P1(x1,x2,…,xn), P2(y1,y2,…,yn)∈Rn
∣P1P2∣=i=1∑n(yi−xi)2
/Define/
定义:设 X 是一个非空集合,∀P1,P2∈X,d(P1,P2) 表达式是一个实数
而且满足下列条件:
-
d(P1,P2)≥0 (非负性)
-
d(P1,P2)=d(P2,P1) (对称性)
-
∀P3∈X (三角形法则)
d(P1,P2)≤d(P1,P3)+d(P2,P3)
称 d(P1,P2) 是 R3 上的一个距离
/additional/
P1(x1,y1,z1)∈R3 , P2(x2,y2,z2)∈R3
d(P1,P2)=∣x2−x1∣+∣y2−y1∣+∣z2−z1∣
验证满足距离定义,但是并非日常所讲距离
(实际上是三维空间中的曼哈顿距离)
· 向量坐标式
矢量的 i, j, k 坐标分解式,简称为坐标式:
a=xi+yj+zk
称为 i, j, k 的坐标分量式
a={x,y,z}=[x,y,z]=(x,y,z)
{x,y,z} 称为坐标式
然后是单位向量有关的部分:
我们想象一个空间向量,与 x , y , z 的夹角为 α , β , γ
z=a⋅k^=∣a∣cosγx=a⋅i^=∣a∣cosαy=a⋅j^=∣a∣cosβ
a={∣a∣cosα,∣a∣cosβ,∣a∣cosγ}={a⋅i^,a⋅j^,a⋅k^}
cosα=∣a∣x=x2+y2+z2xcosβ=∣a∣y=x2+y2+z2ycosγ=∣a∣z=x2+y2+z2z
其中 ∣a∣=x2+y2+z2
cos2α+cos2β+cos2γ=1
a={x,y,z}
a^=∣a∣a=∣a∣1{x,y,z}={cosα,cosβ,cosγ}
称为单位向量
· 坐标运算
a={x1,y1,z1},k是一个常数,则ka={kx1,ky1,kz1}
/proof/
ka=k(x1i^+y1j^+z1k^)=(kx1)i^+(ky1)j^+(kz1)k^={kx1,ky1,kz1}
结束.
不妨给出 b={x2,y2,z2}
a+b=x1i^+y1j^+z1k^+x2i^+y2j^+z2k^=(x1+x2)i^+(y1+y2)j^+(z1+z2)k^={x1+x2,y1+y2,z1+z2}
同理,
a−b={x1−x2,y1−y2,z1−z2}
对于数量级运算:
a⋅b=(x1i^+y1j^+z1k^)⋅(x2i^+y2j^+z2k^)=x1x2+y1y2+z1z2
那对于向量叉乘运算?不难发现如下轮换式:
i^×j^=k^j^×k^=i^k^×i^=j^
根据如上轮换式:
a×b=(x1i^+y1j^+z1k^)×(x2i^+y2j^+z2k^)=x1y2k^−x1z2j^−y1x2k^+y1z2i^+z1x2j^−z1y2i^=(y1z2−z1y2)i^−(x1z2−z1x2)j^+(x1y2−y1x2)k^
不难发现,这个展开式似乎与行列式有关:
a×b=i^x1x2j^y1y2k^z1z2
按第一行展开即可得到结果
/example/ 设a={1,2,3} 和 b={2,1,1}
/proof/
a×b=i^12j^21k^31
=−1i^−(−5)j^+(−3)k^
={−1,5,−3}
· 混合积
设 a={x1,y1,z1},b={x2,y2,z2},c={x3,y3,z3}
积 (a×b)⋅c 称为 a,b,c 的混合积,结果是一个数量。
混合积不能等成:a×b⋅c
(a×b)⋅c=(a×b)⋅c 数量
a×b⋅c=a×(b⋅c) 矢量
混合积 (a×b)⋅c=
(a×b)⋅c=[(y1z2−z1y2)i−(x1z2−z1x2)j+(x1y2−y1x2)k ](x3i^+y3j^+z3k^)=(y1z2−z1y2)x3+(x1z2−z1x2)y3+(x1y2−y1x2)z3
=x3x1x2y3y1y2z3z1z2=x1x2x3y1y2y3z1z2z3
/example/
(a×b)⋅c=−(c×b)⋅a
(a×b)⋅c=(b×c)⋅a
证明 (a×b)⋅c=a⋅(b×c)
/proof/
证:右边 =a⋅(b×c)
=(b×c)⋅a
=−(a×c)⋅b
=(a×b)⋅c
= 左式
然后给出混合积性质:
/property/
a , b , c共面的充要条件是 (a×b)⋅c=0
⇔x1x2x3y1y2y3z1z2z3=0
若a={x1,y1,z1} , b={x2,y2,z2} , c={x3,y3,z3}, 有下列性质:
性质1
a⊥b⇔a⋅b=0
⇔x1x2+y1y2+z1z2=0
性质 2
a∥b⟺a×b=0
⟺b=0, a=λb⟺x2x1=y2y1=z2z1
向量中分量可以一个或两个为 0
比如:
x2x1=0y1=z2z1=λ
“建立形式上的比”
可以推出 y1=0⋅λ=0
· 几何意义
向量叉乘几何意义:
∣a×b∣=∣a∣∣b∣sinθ , S=21∣a×b∣ (与 a , b , θ 相关的平行四边形面积)
混合积的几何意义:
∣(a×b)⋅c∣=∣a×b∣∣c∣∣cos⟨a×b,c⟩∣=∣a×b∣∣c∣∣cosθ∣
VO−ABC=21S⋅h=61∣(a×b)⋅c∣
Fragment 2 平面与直线方程
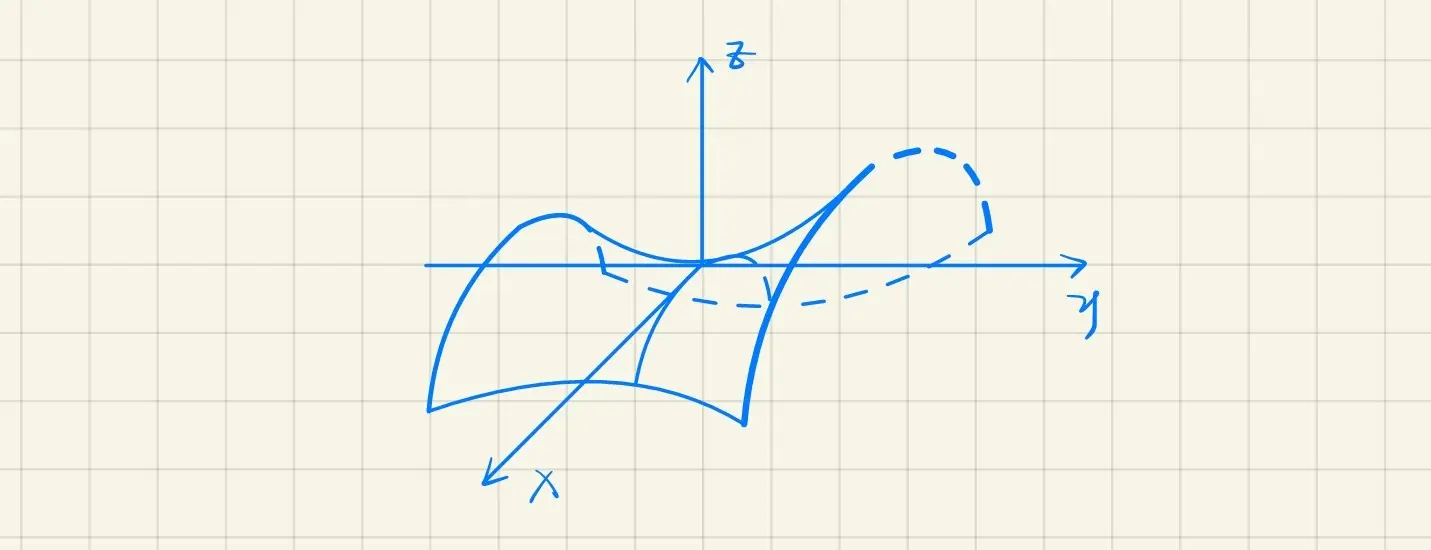
· 空间曲面曲线方程
/Define/
设 Σ(Ω) 是空间一张曲面,F(x,y,z)=0 是一个三元方程,
M(x1,y1,z1)∈Σ⇒F(x1,y1,z1)=0
反之,若对 M(x1,y1,z1) 有 F(x1,y1,z1)=0
⇒M(x1,y1,z1)∈Σ
知 { M∣ M∈Σ } 与 {(x,y,z)∣F(x,y,z)=0} 建立一一对应
称 f(x,y,z)=0 是曲面 Σ 的方程
而曲面 Σ 是方程 F(x,y,z)=0 表示的曲面
方程 f(x,y,z)=0 称为曲面 Σ 的一般方程
如果从方程可以解出 z=f(x,y),称为曲面 Σ 的显函数表达式
求曲面 Σ 方程的方法:
设 M(x,y,z) 是 Σ 上任意一点,找到 M 点满足的等式
⇔F(x,y,z)=0
就是曲面 Σ 的方程
曲线 Γ 的方程,用
{F(x,y,z)=0G(x,y,z)=0
称为曲线方程的一般式
空间曲线Γ参数式:
Γ=⎩⎨⎧x=x(t)y=y(t)z=z(t)
t为参数
空间曲面Σ参数式:
Σ=⎩⎨⎧x=x(u,v)y=y(u,v)z=z(u,v)
u,v为参数
· 平面与直线方程
· 平面方程
1.点法式
设平面π经过已知点P0(x0,y0,z0),且与非零常矢量n={A,B,C}垂直,求平面π的方程:
设 n=(A,B,C) 是平面 π 的法向量,P0=(x0,y0,z0) 是平面上一点,则平面 π 的点法式方程为:
A(x−x0)+B(y−y0)+C(z−z0)=0
这就是所求的平面方程,这个方程称为平面 π 的点法式方程。
求平面 π 法向量 n 的方法:
-
若 a∈π,b∈π,a×b ,则 n=a×b
-
若 a∈π,b∥π,a×b ,则 n=a×b
-
若 a∥π,b∥π,a=b ,则 n=a×b
2.一般式:
由平面方程的点法式 A(x−x0)+B(y−y0)+C(z−z0)=0
⇒Ax+By+Cz−(Ax0+By0+Cz0)=0
设 D=−(Ax0+By0+Cz0) ⇒Ax+By+Cz+D=0
其中 A, B, C 不全为 0。
反之,若 Ax+By+Cz+D=0 其中 A, B, C 不全为 0。
不妨设 A=0,取 y=y0,z=z0
x=A−By0−Cz0−D≜x0
得到了方程的一组解 (x0,y0,z0)。
有 Ax0+By0+Cz0+D=0
⇒D=−(Ax0+By0+Cz0)
⇒Ax+By+Cz+(Ax0+By0+Cz0)=0
⇒A(x−x0)+B(y−y0)+C(z−z0)=0
知 Ax+By+Cz+D=0 表示一个平面。
即全体平面组成的集合
与 {Ax+By+Cz+D=0∣A,B,C∈R,不全为0}
建立了一一对应。
所以 Ax+By+Cz+D=0 ,称为平面方程的一般式。
(1) 若平面 π 经过原点,方程为 Ax+By+Cz=0。
(2) 若平面 π 平行于 Oz 轴,
{A,B,C}⋅{0,0,1}=0 , C=0
方程为 Ax+By+D=0
(3) 若平面 π 经过 Oz 轴,方程为 Ax+By=0
3.截距式
若平面方程为
ax+by+cz=1
且 a,b,c=0 ,称为截距式,该平面经过点 (a,0,0), (0,b,0), (0,0,c)。
a, b, c 称为平面方程在 x 轴、y 轴、z 轴的截距。
VO−ABC=61∣abc∣
平面的一般式 Ax+By+Cz+D=0 写成截距式,要求 ABCD=0。
⇒−ADx+−BDy+−CDz=1
4.三点式
若平面 π 经过不在同一条直线上的三点 M1(x1,y1,z1),M2(x2,y2,z2),M3(x3,y3,z3),求平面的方程。
/proof/
解法一:由条件知
M1M2⊂π,M1M3⊂πM1M2=M1M3
n=M1M2×M1M3=ix2−x1x3−x1jy2−y1y3−y1kz2−z1z3−z1
按第一行展开,求出 n。
再经过 M1,然后用点法式。
解法二:
∀M(x,y,z)∈π
MM1,M1M2,M1M3 are coplanar
混合积为 0
x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1
按第一行展开,写成点向式。
/example/ 平面 π 经过 M1(1,1,1), M2(2,2,2), M3(1,2,3),求 π 的方程
解法一
M1M2=(1,1,1),M1M3=(0,1,2)
n=i10j11k12
n={1,−2,1}
∴ 平面 π 的方程为
(x−1)−2(y−1)+(z−1)=0
解法二
平面 π 的方程为
x−110y−111z−112=0
即
(x−1)−2(y−1)+(z−1)=0
· 直线方程
1.点向式
设 L 经过已知点 M0(x0,y0,z0),且与非零的常矢量 v={l,m,n} 平行,求 L 的方程。
M0(x0,y0,z0)v=0⇒L
得 ∀M(x,y,z)∈L , M0M⊂L
由 v∥L⟺M0M∥v
由 v=0,则
lx−x0=my−y0=nz−z0
这就是所求直线 L 的方程,称为点向式(对称式), v 称为 L 的方向向量
2.直线的参数式
⎩⎨⎧x=x0+lty=y0+mtz=z0+nt
t 为参数,−∞<t<+∞
3.两点式
若直线 L 经过不同的两点 M1(x1,y1,z1) 和 M2(x2,y2,z2),求 L 的方程。
得 v=M1M2=(x2−x1,y2−y1,z2−z1) , L 经过 M1(x1,y1,z1)。
由点向式,得 L 的方程为
x2−x1x−x1=y2−y1y−y1=z2−z1z−z1
4.一般式
L:{A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0
要求两平面不平行,即
[A1,B1,C1]×[A2,B2,C2]=0
L 的方向向量
v=iA1A2jB1B2kC1C2
直线方程常用点向式
/question/ 如何求直线 L 的方向向量
/proof/
-
若 L⊥a, L⊥b, 且 a×b
v=a×b
-
若 L⊥a, L∥π, π 的法向量为 n
n⊥π,L∥π⇒L⊥n
∴v=a×n
· 平面方程的平面束
经过直线 L={A1x+B1y+C1z+D1A2x+B2y+C2z+D2=0=0
的平面方程一定可以写成
λ(A1x+B1y+C1z+D1)+μ(A2x+B2y+C2z+D2)=0
其中,λ, μ 为待求的参数,称为平面束方程。
· 距离问题
· 点到平面距离
设平面 π=Ax+By+Cz+D=0
P(x1,y1,z1) 是空间一点,求 P 到 π 的距离 d
d=A2+B2+C2∣Ax1+By1+Cz1+D∣
设P∈π,P=P0
d=∣P1P⋅n=∣n∣∣P1P⋅n∣=A2+B2+C2∣A(x−x1)+B(y−y1)+C(z−z1)∣=A2+B2+C2∣Ax+By+Cz−(Ax1+By1+Cz1)∣=A2+B2+C2∣Ax1+By1+Cz1+D∣
· 点到直线的距离
设
L:lx−x0=my−y0=nz−z0
P1(x1,y1,z1)是空间一点,求P1到L的距离
d=∣P′P1∣=∣v∣∣P0P1×v∣=aSparallelogram
· 直线方程转化
(1) 点向式转化为一般式
根据
lx−x0=my−y0=nz−z0
消元:
⇒⎩⎨⎧lx−x0my−y0=my−y0=nz−z0
⟺{m(x−x0)−l(y−y0)n(y−y0)−m(z−z0)=0=0
(2) 一般式转化为点向式
由 {A1x+B1y+C1z+D1A2x+B2y+C2z+D2=0=0
方法一:L 的方向向量
v={A1,B1,C1}×{A2,B2,C2}=iA1A2jB1B2kC1C2
求出 L 的一个点 P0(x0,y0,z0),用点向式写出方程
方法二:消元法
/example/ 转化为点向式:
L={x+y+zx+2y+3z=1=0
/proof/
选取 z 为参数。
消去 x:(2) - (1)
y+2z=−1,z=−2y+1
消去 y:(2) - (1) × 2
−x+z=−2,z=x−2⇒1x−2=−2y+1=1z−0
知直线经过 (2,−1,0),
方向向量 v={1,−2,1}
/example/ L={x+y+zx−y+z=1=2
/proof/
以 z 为参数
消去 y:(1) + (2)
2x+2z=3,z=−1x−23
消去 x:(1) - (2)
2y=−1⇒2y+1=0⇒z=02y+1=0y+21
形式上的比
−1x−23=0y+21=1z−0
· 直线投影问题
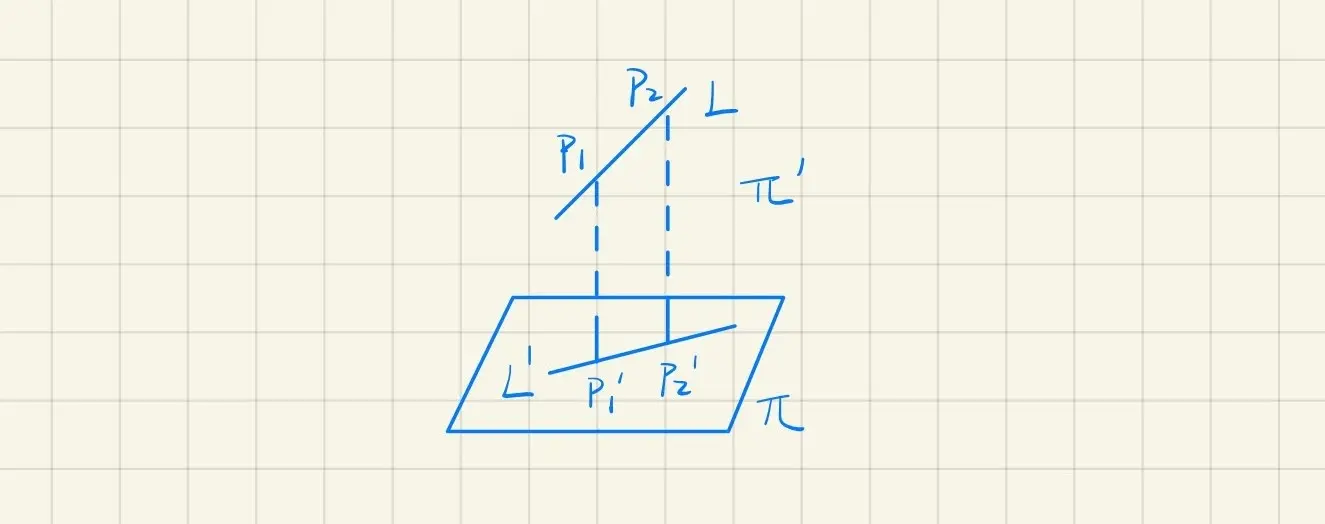
/example/ 求直线 L={x+y−z−1x−y+z+1=0=0 在平面 π=x+y+z=0 上投影直线 L′ 的方程

解法一:直线的两点式
L 上任取 P1, P2 两点, P1 与 π 点向式,得到 P1P1′,与 π 交于 P1′ , P2 同理。
解法二:直线的一般式
L′ 为 π 与 π′ 联立,点法式求 π′=L 上任取一点 P1
L 的方向向量 l={1,−1,1}×{1,−1,1} 与 π 的法向量 n={1,1,1} 叉乘,得 π′ 的法向量
解法三:设 L 与 L′ 确定的平面为 π′
设 π′ 的方程为:
λ(x+y−z−1)+μ(x−y+z+1)=0
π′ 的法向量 n′={1,1,1}
由 (λ+μ)x+(λ−μ)y+(μ−λ)z=0
n′={λ+μ,λ−μ,μ−λ}
由 n⊥n′,有
λ+μ+λ−μ+μ−λ=0
μ=−λ
2λy−2λz−2λ=0
⇒y−z−1=0
∴L′={x+y+zy−z−1=0=0
· 直线平面关系

L1:l1x−x1=m1y−y1=n1z−z1
L2:l2x−x2=m2y−y2=n2z−z2
直线 L1 和 L2 的关系
-
若 (v1×v2)⋅M1M2=0 ⟺L1,L2 共面
-
若 (v1×v2)⋅M1M2=0, 且 v1=v2 ⟺L1,L2 相交
-
v1∥v2⟺L1∥L2
-
若 (v1×v2)⋅M1M2=0 ⟺L1,L2 为异面直线
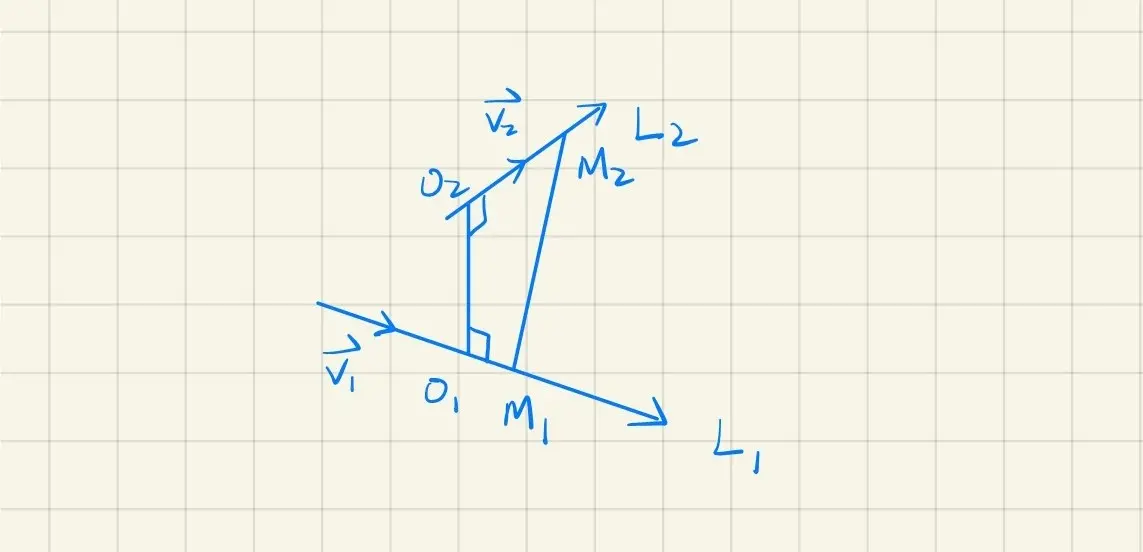
· 异面直线距离
若 L1,L2 为异面直线,求 ∣O1O2∣ (公垂线)

解法一 过O1 作L2′∥L2
由L1,L2′ 构成一平面,L2 任意一点到平面一点均相等。
问题:如何确定O1
解法二 过M1 作L2′∥L2
则高度∣O1O2∣=∣M1M2⋅n0∣ ,其中,n0 为v1×v2 的单位矢量
n0=∣v1×v2∣v1×v2
解法三 精彩一刻
∣O1O2∣=∣v1×v2∣∣(v1×v2)⋅M1M2∣
h=SV
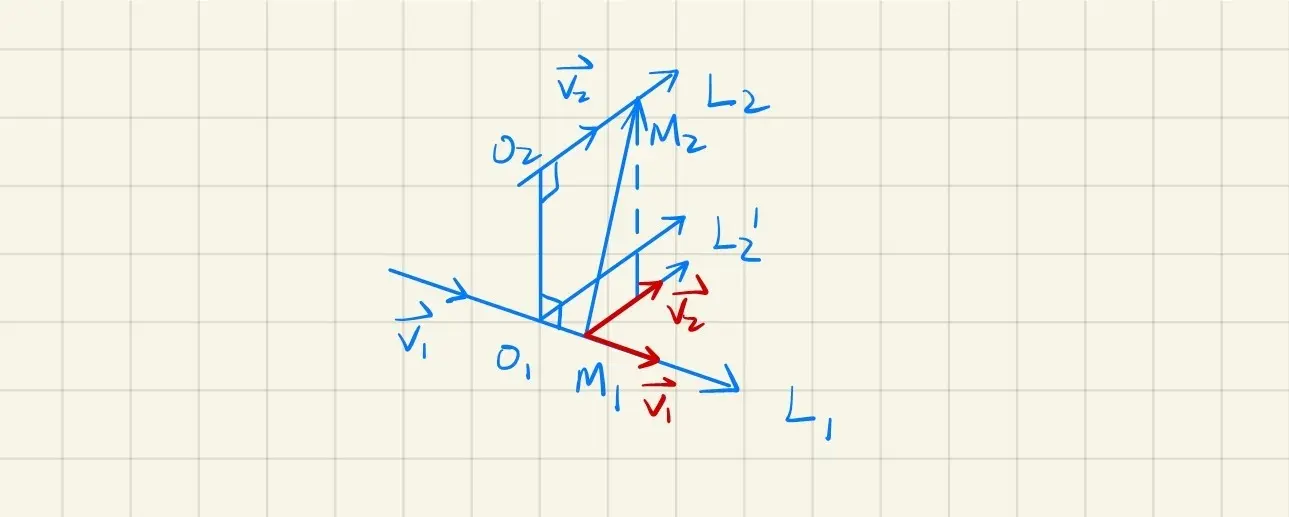
/question/ 求O1O2 的方程
设O1O2 与L1 确定的平面为π1
M1∈π1,n1=(v1×v2)×v1
点法式写出π1 方程
设O1O2 与L2 确定的平面为π2
M2∈π2,n2=(v1×v2)×v2
点法式写出π2 方程
转化思路,使用参数方程:
不妨设
L1=⎩⎨⎧xyz=x1(s)=y1(s)=z1(s)L2=⎩⎨⎧xyz=x2(t)=y2(t)=z2(t)
设 O1(x1(s),y1(s),z1(s))
设 O2(x2(t),y2(t),z2(t))
O1O2∥v1×v2={a,b,c}=0,有
ax2(t)−x1(s)=by2(t)−y1(s)=cz2(t)−z1(s)
· 向量表示夹角
求 L1 与 L2 的夹角 θ (0≤θ≤2π)
(1) 0≤<v1,v2>≤2π
cosθ=cos<v1,v2>=∣v1∣∣v2∣v1⋅v2=∣v1∣∣v2∣∣v1⋅v2∣
(2) 2π≤<v1,v2>≤π
cosθ=cos[π−<v1,v2>]=−cos<v1,v2>=−∣v1∣∣v2∣v1⋅v2=∣v1∣∣v2∣∣v1⋅v2∣
总之,
cosθ=∣v1∣∣v2∣∣v1⋅v2∣(0≤θ≤2π)
(v1=0, v2=0)
2.求平面 π1 与 π2 的夹角 θ (0≤θ≤2π)
cosθ=∣n1∣∣n2∣∣n1⋅n2∣
3.直线 L 与平面 π 的夹角 θ (0≤θ≤2π)
⟺sinθ=∣v1∣∣v2∣∣v1⋅v2∣(0≤θ≤2π)
Fragment 3 一般曲面方程
· 球面
设一动点到一定点 P0(x0,y0,z0) 的距离为 R,求此轨迹方程。
/solution/
设 P(x,y,z) 是轨迹上任意一点。
由条件知,∣P0P∣=R⟺∣P0P∣2=R2
(x−x0)2+(y−y0)2+(z−z0)2=R2
表示以 P0(x0,y0,z0) 为中心,半径为 R 的球面。
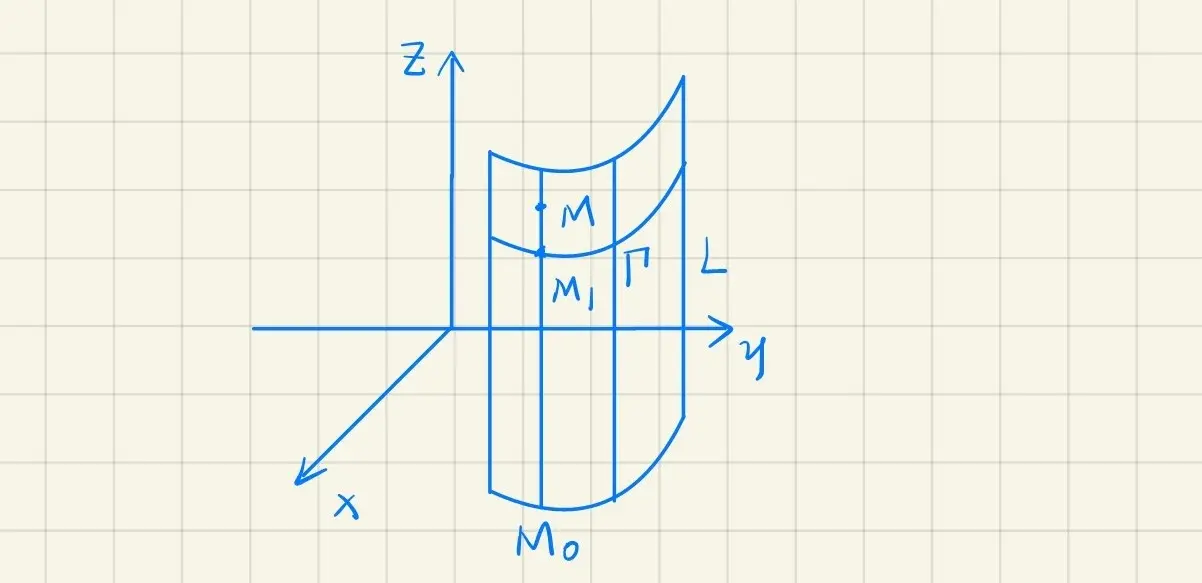
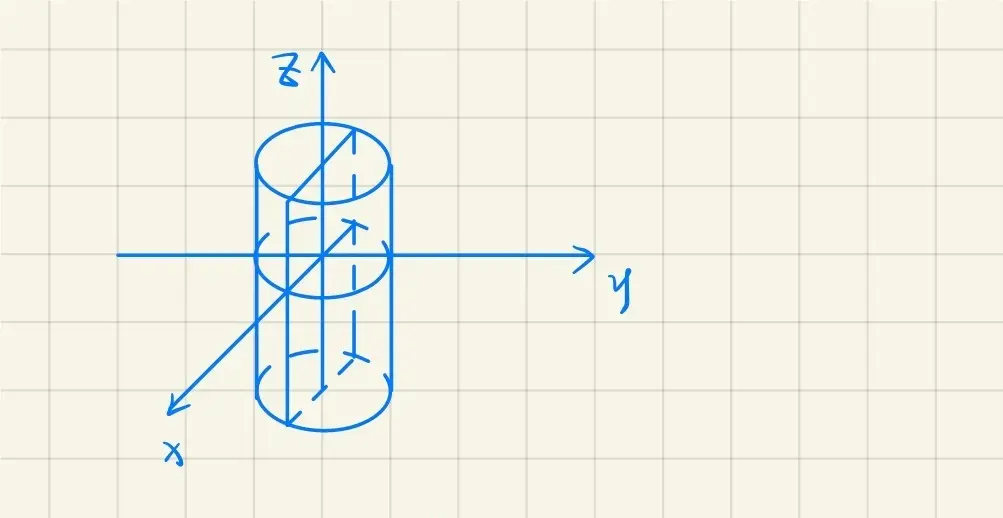
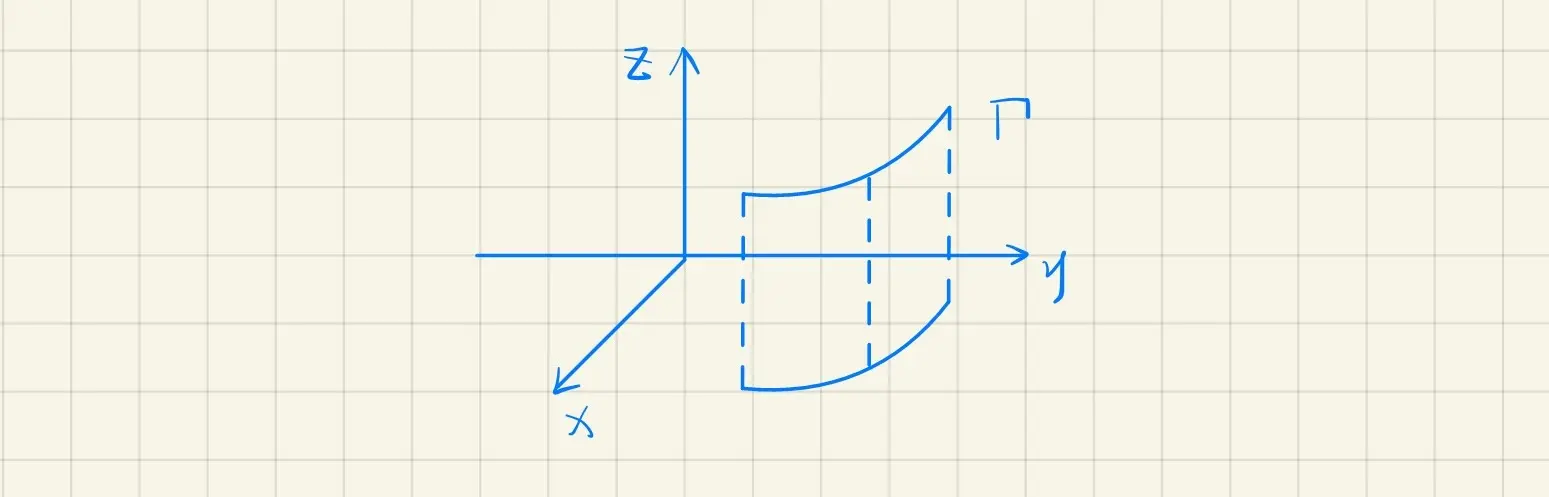
· 柱面
/Define/
设 Γ 为一定曲线,ν 为一个非零的常矢量,L 为一动直线,当 L 沿着曲线 Γ(L 与 Γ 相交)且与 ν 平行移动所产生的曲面,称为柱面,称 L 为母线,Γ 称为准线
请问:x2+y2=R2 (R>0,常数) 表示什么?
/example/ 求以曲线 {f(x,y)=0z=k(Constant) 为准线,母线平行于 Oz 轴的柱面的方程

设 M(x,y,z) 是柱面上任意一点。
过 M 点作平行于 Oz 轴的母线与 Γ 交于 M1(x1,y1,z1),有
{f(x1,y1)z1=0=k
因
{xy=x1=y1
∴M 点坐标满足方程为 f(x,y)=0
就是该曲面的方程
曲面 f(x,z)=0 表示什么?
柱面,f(x,z)=0 与 y=k(常数)交线为准线,母线平行于 Oy 轴。
知 x2+y2=R2,表示以
{x2+y2z=R2=0
为准线,母线平行于 Oz 轴的圆柱面。

/example/ y=x2 的曲面
/proof/
{yz=x2=0
为准线,母线平行于 Oz 轴的抛物柱面

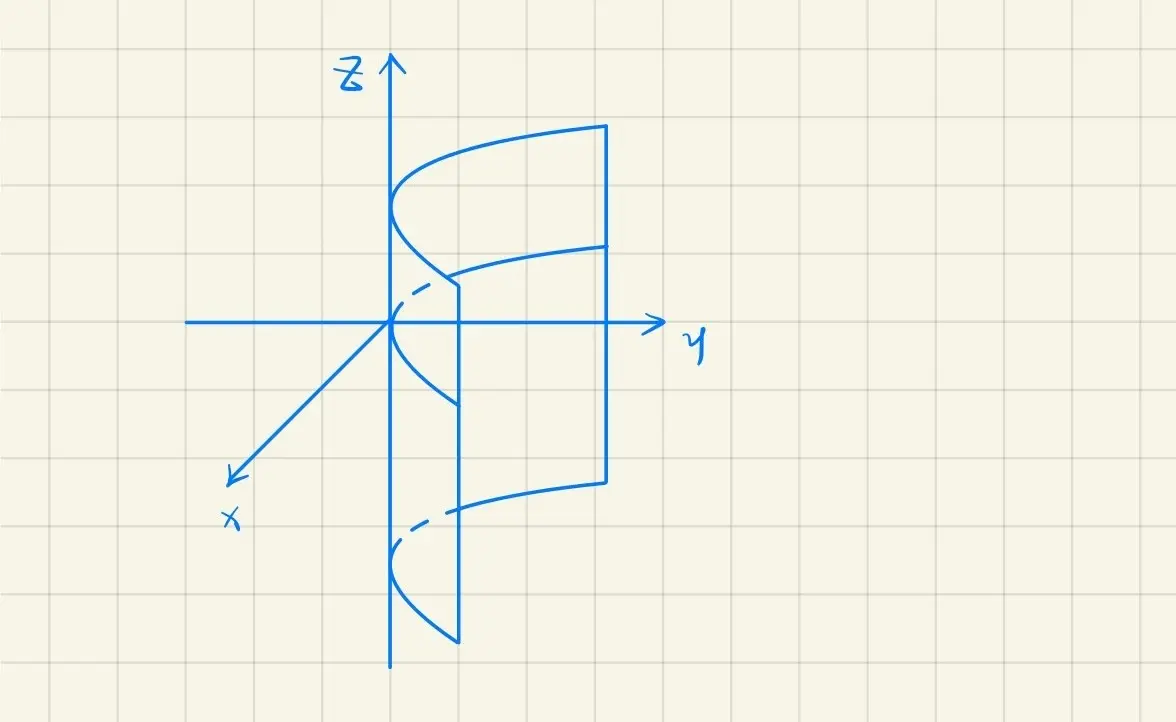
平行于 Oz 轴的平面,方程为 Ax+By+D=0 (可看成一柱面)
/example/ 侧面 x+y=1 表示的平面
/proof/
以 {x+yz=1=0 为准线,
母线平行于 Oz 轴。
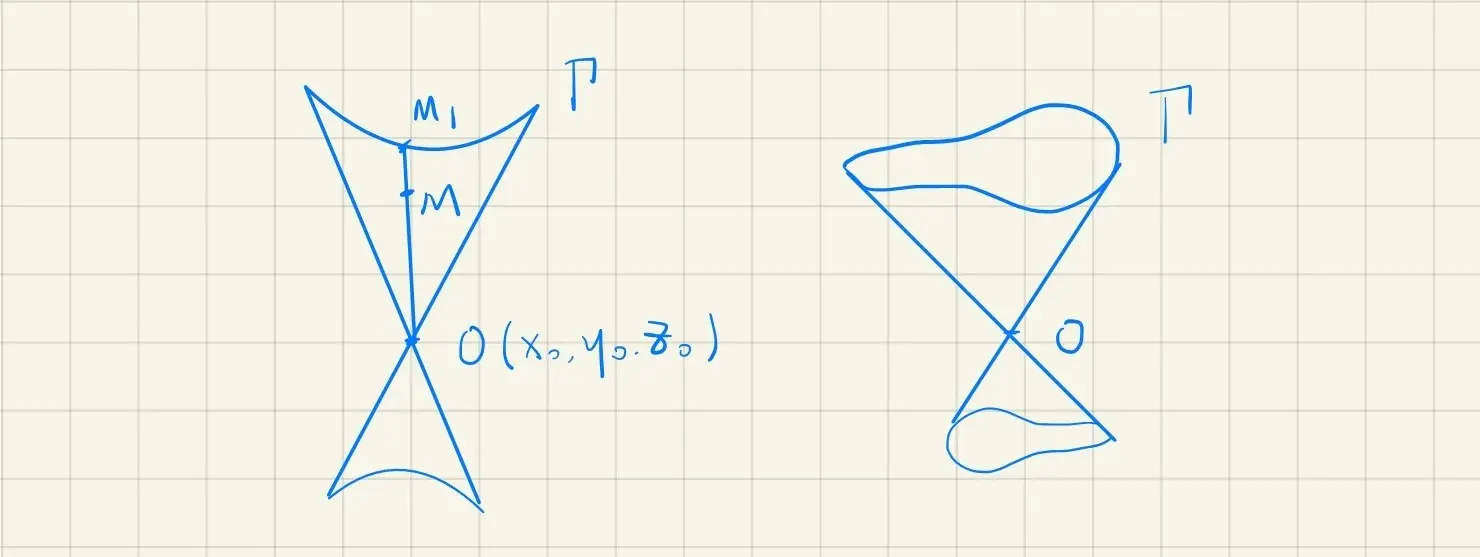
· 锥面
设 O 是空间一定点,Γ 是一定曲线,O∈/Γ,有一动直线 L 经过 O 点,与 Γ 相交,设 Γ 移动所生成的曲面称为锥面,
O 点称为顶点,动直线称为母线,Γ 称为准线。

求锥面方程的方法:
设 M 点是锥面上任意一点,连接 OM,与 Γ 相交于 M1(x1,y1,z1),
M1(x1,y1,z1) 满足 Γ 的方程,OM∥OM1⟺ 向量对应成比例。
· 旋转曲面
/example/ 求曲线 Γ={f(y,z)=0x=0 绕 Oz 轴旋转一周所形成的旋转曲面的方程。

/proof/
设 M(x,y,z) 是曲面上任意一点,
则 M(x,y,z) 是由曲线 Γ 上某点 M1(x1,y1,z1) 旋转形成的圆周上的一点。
已知
{f(y1,z1)x1=0=0
z=z1,∣O1M∣=∣O1M1∣
x2+y2=x12+y12=y12
y1=±x2+y2
知曲面的方程为 f(±x2+y2,z)=0
/example/
{f(y,z)x=0=0
绕 Oy 轴旋转得到曲面方程为 f(y,±z2+x2)
/example/
{f(x,y)z=0=0
绕 Ox 轴旋转得到曲面方程为 f(x,±y2+z2)
/example/ a2x2+b2y2−c2z2=1 是否是旋转曲面?
是旋转曲面
它是如何形成的?
⎩⎨⎧b2y2−c2z2x=1=0
绕 Oz 轴旋转所得到
验证:a2(±y2+x2)2−c2z2=1
⟺a2x2+a2y2−c2z2=1

也可以看成由 ⎩⎨⎧a2x2−c2z2y=1=0
绕 Oz 轴旋转得到
验证:a2x2+y2−c2z2=1
即 a2x2+a2y2−c2z2=1

· 绕轴旋转曲面方程求解
把曲线Γ表示为
⎩⎨⎧xyz=f(z)=g(z)=z
解 设M(x,y,z)是曲面上任意一点。
M由Γ上某点M1(x1,y1,z1)绕Oz轴
旋转形成的圆周上的一点,有
{x1y1=f(z1)=g(z1)
z=z1,x2+y2=x12+y12=f2(z1)+g2(z1)=f2(z)+g2(z)
就是我们所求的曲面方程。
Fragment 4 二次曲面
面一般方程F(x,y,z)=0表示的曲面:用一系列平行于坐标平面的平面去截这个曲面,截口是一个曲线
/example/
{f(x,y,z)z=0=k⟺{f(x,y,k)z=0=k
是一个曲线,由一系列的曲线,可以画出曲面的草图。
这种方法称为平面截割法。
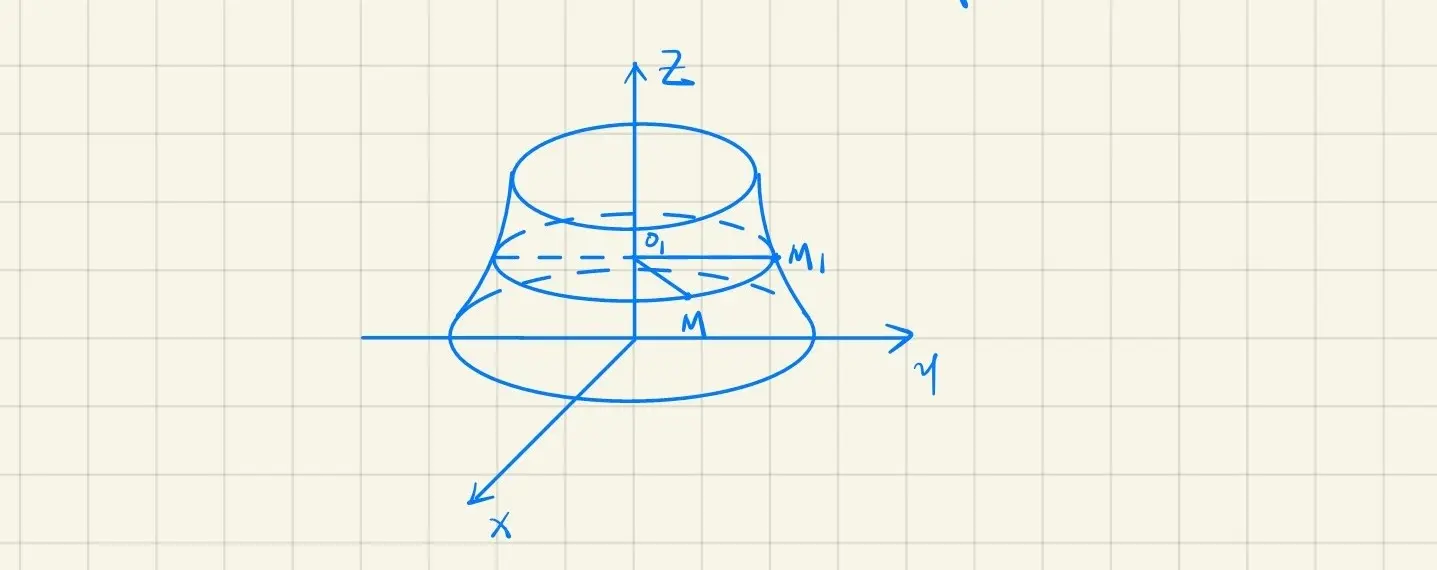
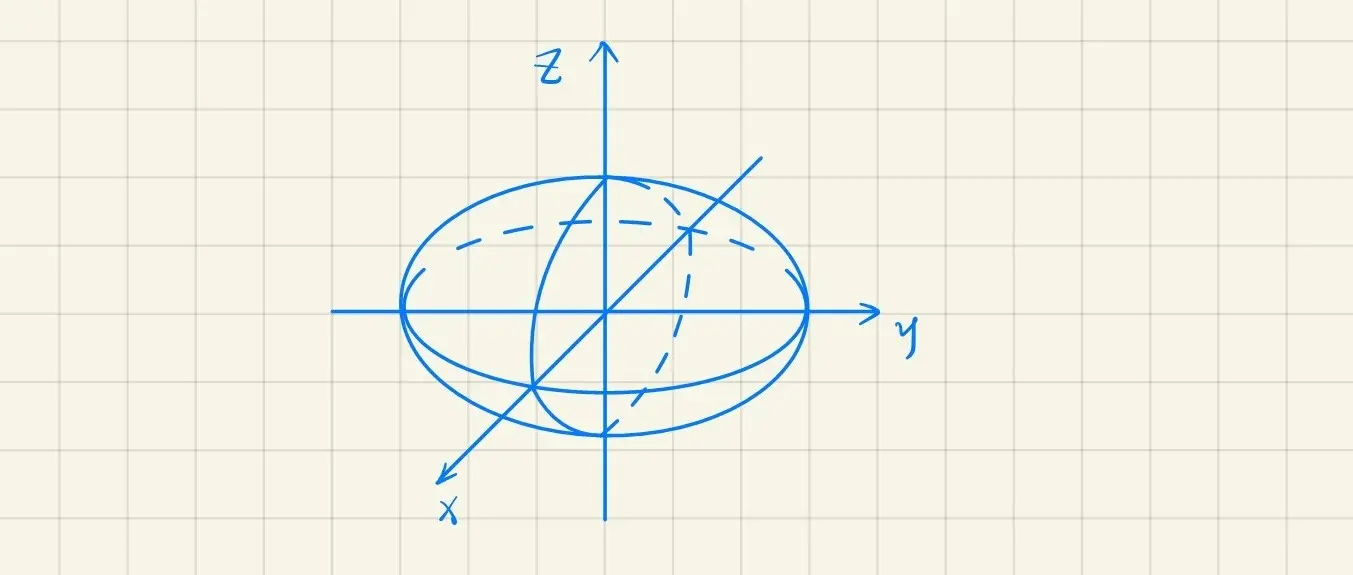
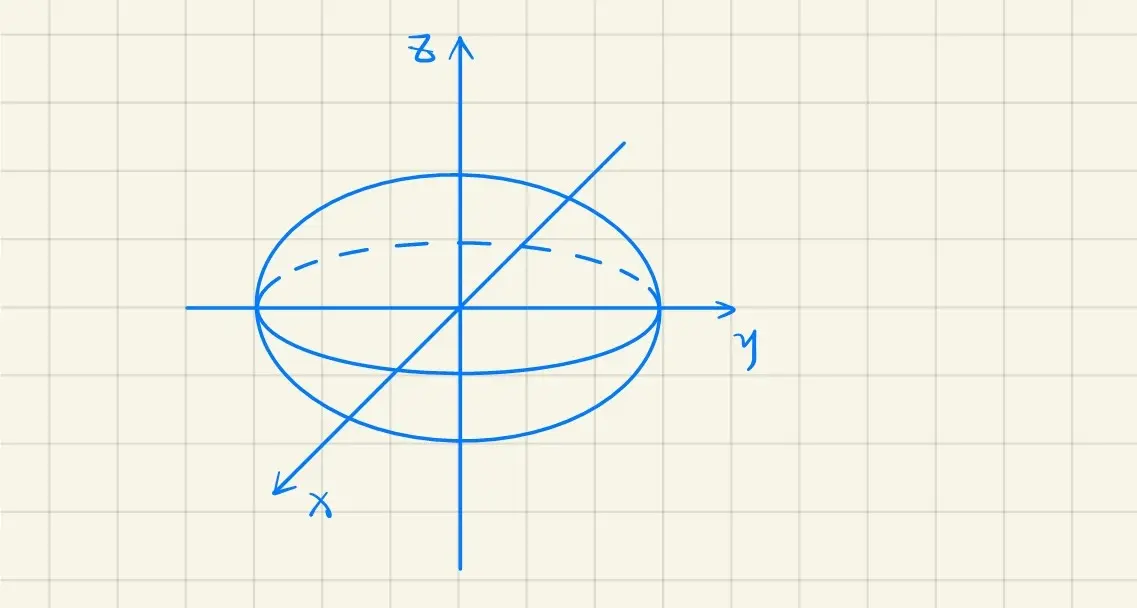
· 椭球面
a2x2+b2y2+c2z2=1(a>0,b>0,c>0)
由如下方程组
⎩⎨⎧a2x2+b2y2+c2z2z=1=k∣k∣<c
可以推出
⟺⎩⎨⎧a2x2+b2y2z=1−c2k2=k
⟺⎩⎨⎧(a1−c2k2)2x2+(b1−c2k2)2y2=1z=k∣k∣<c

(由特殊图画一般曲面的草图)
当 a=b 时,椭球面方程为
a2x2+a2y2+c2z2=1
是旋转曲面,是由 ⎩⎨⎧a2y2+c2z2x=1=0 绕 Oz 轴旋转所得曲面

适用情况:方程中有两个变量的平方,符号相同,画草图时可令其系数相同,变为旋转曲面。
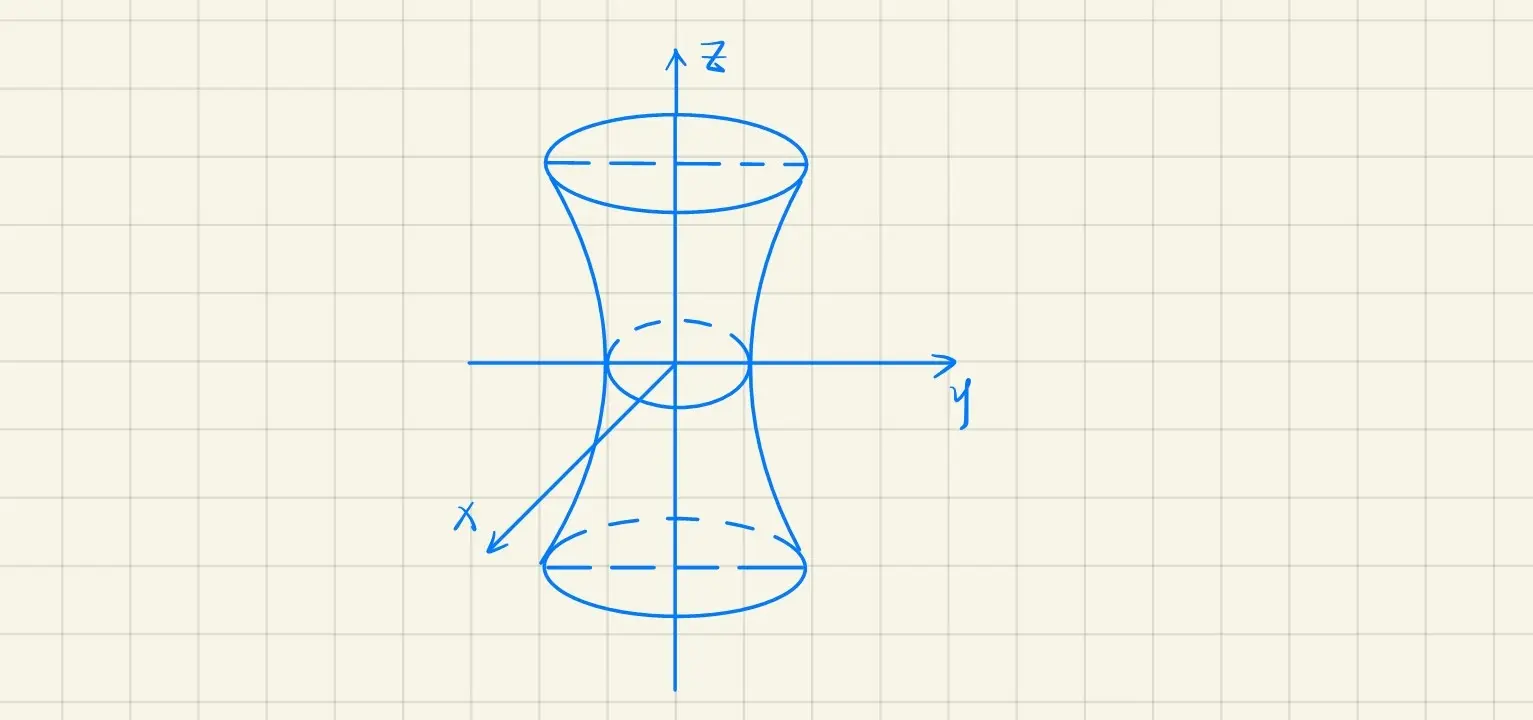
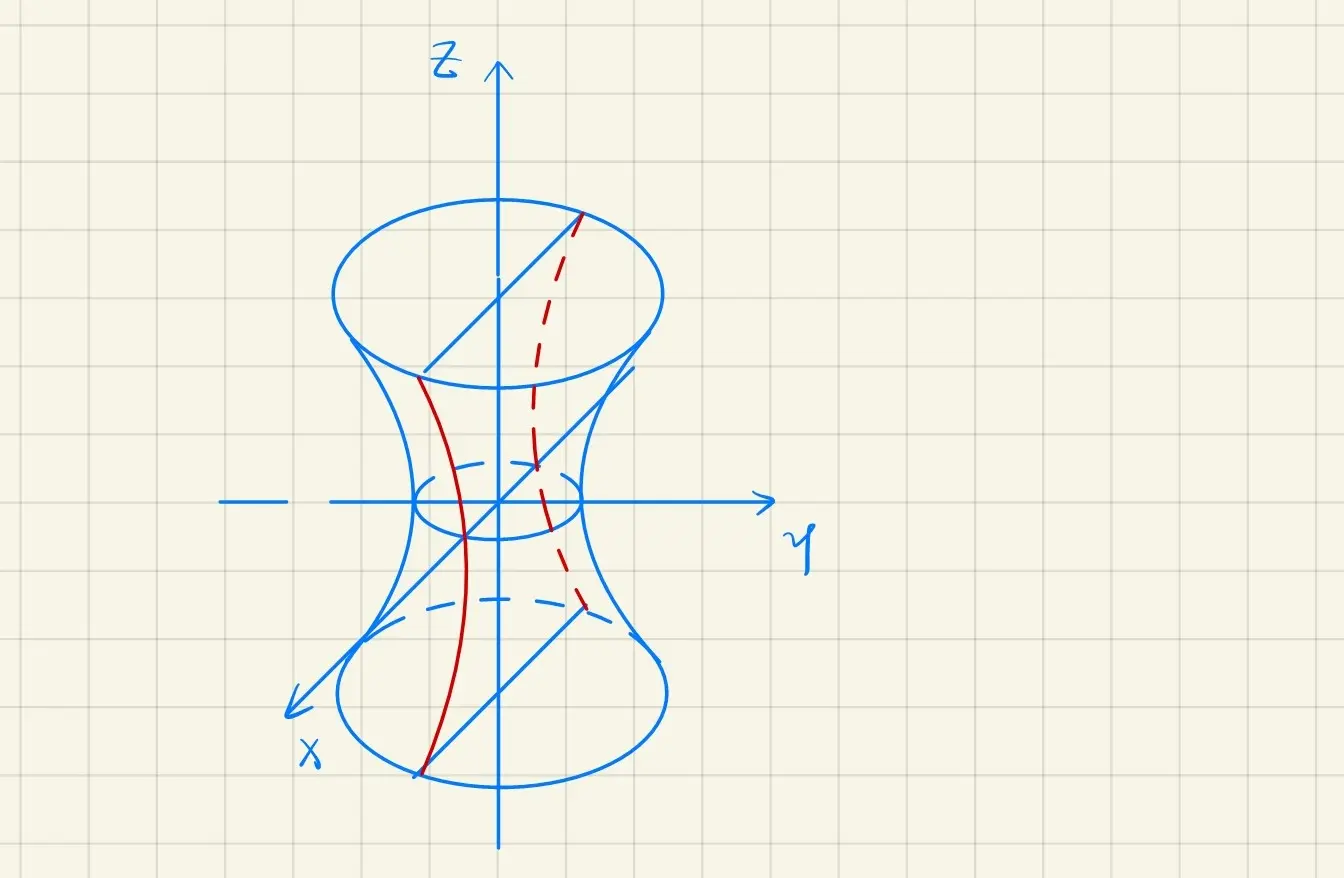
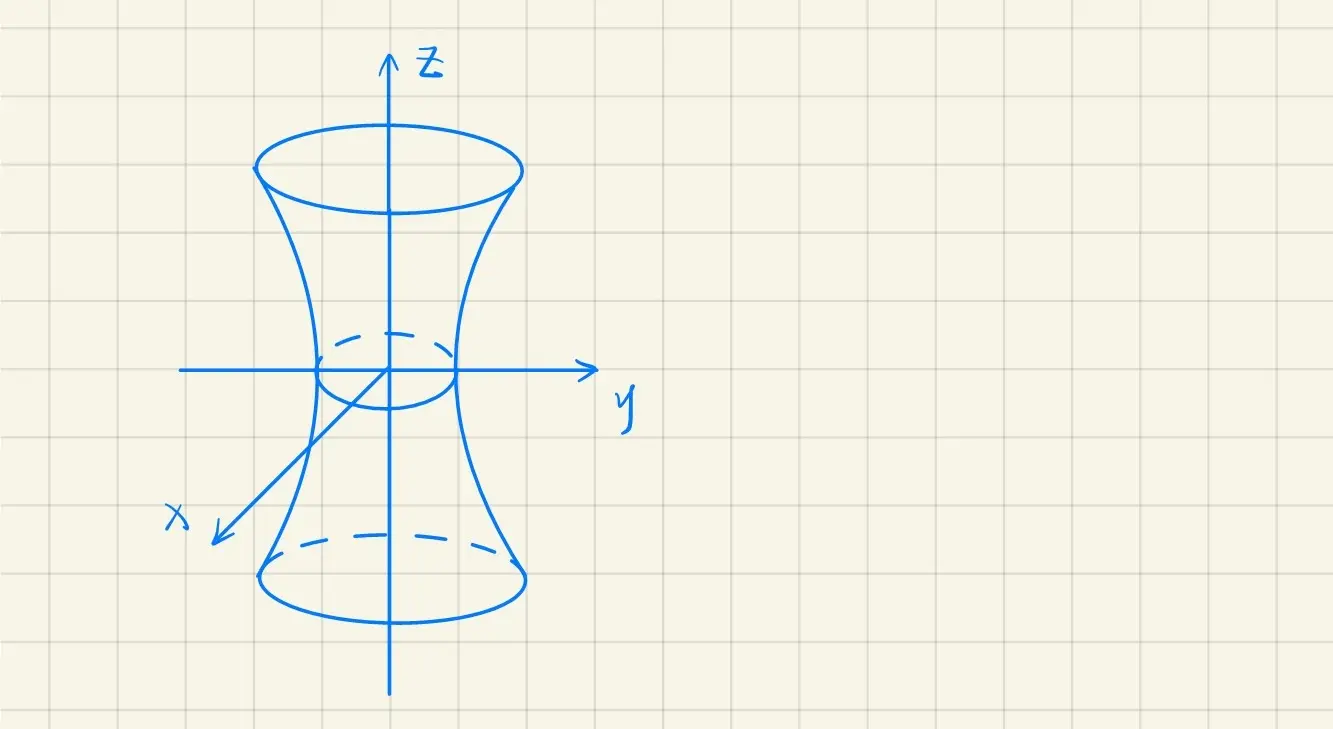
· 单叶双曲面
a2x2+b2y2−c2z2=1
令 a=b,得
a2x2+a2y2−c2z2=1
是旋转曲面,由
⎩⎨⎧a2x2−c2z2x=1=0
绕 Oz 轴旋转得到

· 双叶双曲面
a2x2+b2y2−c2z2=−1
令 a=b,得
⎩⎨⎧a2y2−c2z2x=−1=0
绕 Oz 轴旋转所得曲面

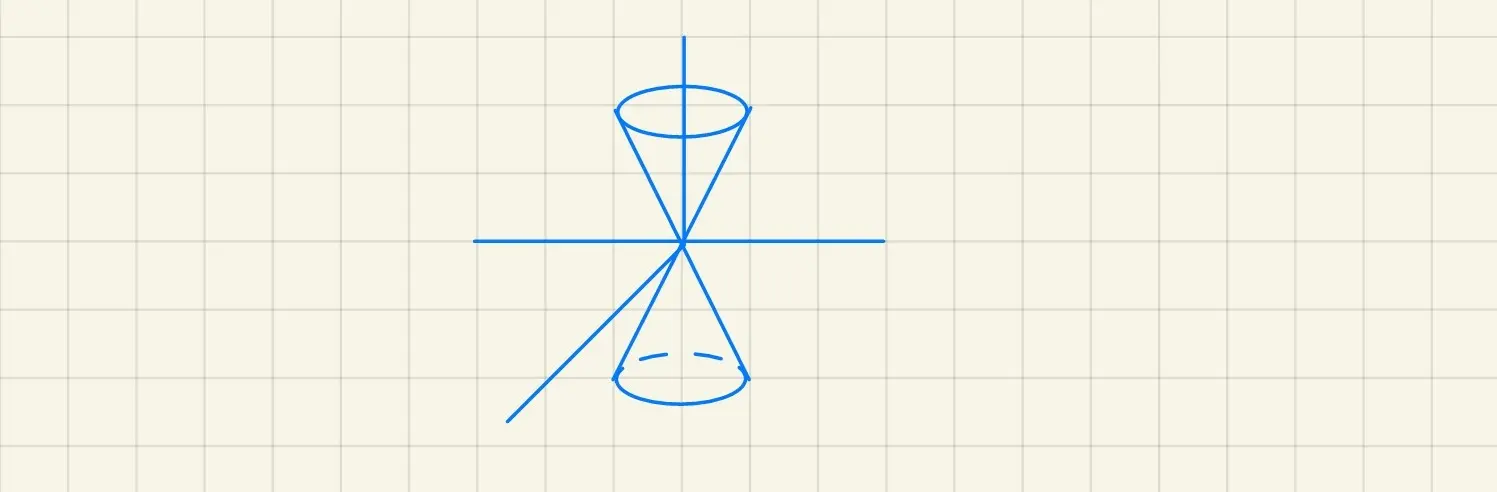
· 二次锥面
a2x2+b2y2−c2z2=0
令 a=b,有
a2x2+a2y2−c2z2=0
由
⎩⎨⎧a2y2−c2z2x=0=0
绕 Oz 轴旋转所得曲面
⟺⎩⎨⎧ay+czx=0=0or⎩⎨⎧ay−czx=0=0

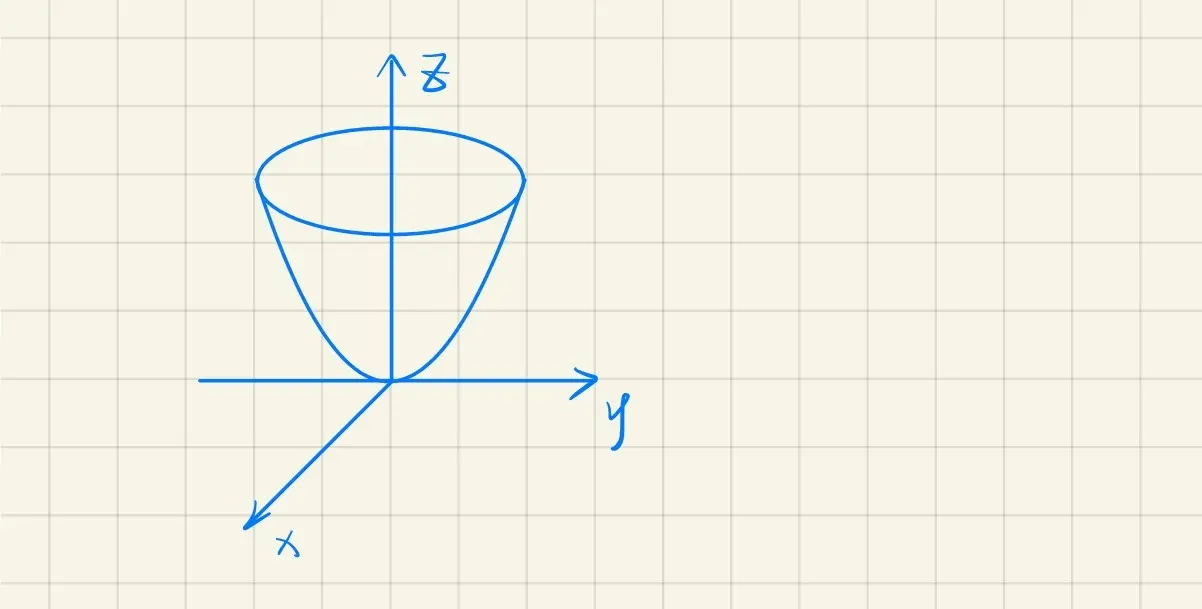
· 椭圆抛物面
z=a2x2+b2y2
当 a=b 时,z=a2x2+a2y2 ,由 ⎩⎨⎧zx=a2y2=0 绕 Oz 轴旋转所得曲面

· 双曲抛物面
z=−a2x2+b2y2
由 ⎩⎨⎧zx=−a2x2+b2y2=0
⟺⎩⎨⎧zx=b2y2=0
(1) 是抛物线
根据
⎩⎨⎧zy=−a2x2+b2y2=k
⟺⎩⎨⎧z−b2k2y=−a2x2=k
(2) 是抛物线,顶点是 (0,k,b2k2)
在抛物线 (1) 上
⎩⎨⎧zz=−a2x2+b2k2=k

Fragment 5 空间曲线研究方法
1.画曲线的草图
注意把方程组进行恒等变形,以使清楚知道是什么曲线,如何画草图
/example/
⎩⎨⎧x2+y2+z2x2+y2+z2=1=z+43
面该曲线的图形
/proof/
(2) - (1): 0=z−41
⎩⎨⎧x2+y2z=1615=41
2.求曲线Γ
{F(x,y,z)G(x,y,z)=0=0
在xoy平面上投影曲线 Γ′ 的方程

/proof/
设 Γ′ 即为准线 Γ,母线平行于 Oz 轴
的线形成的柱面,与 xoy 平面 (z=0) 的交线
由 {F(x,y,z)G(x,y,z)=0=0
消去 z,得到 H(x,y)=0
知该曲面是以 Γ 为准线,
母线平行于 Oz 轴的柱面,
则投影曲线 Γ′:
Γ′:{H(x,y)z=0=0
向量代数结束,大家新年快乐