Chapter 1 质点运动学

Fragment 0 基础知识总结

· 位移 速度 加速度

位置矢量（位矢）：建立直角坐标系后，物体的位置可用坐标 $A(x,y,z)$ 表示，向量 $\vec{r}=\overrightarrow{OA}$ 就称为位置矢量，也记为 $\vec{r}=x\vec{i}+y\vec{j}+z\vec{k}$ .

运动函数：运动函数就是质点坐标 $x,y,z$ 随 $t$ 的变化关系，将 $t$ 消掉判断运动轨迹

位移和路程：

• 物体的位置变化称为位移 $\Delta \vec{r}$ ，实际运动路径长称为路程 $\Delta s$
• $\Delta \vec{r}$ 是位移，$|\Delta \vec{r}|$ 是位移大小， $\Delta r$ 是物体到原点距离变化
• 只有 $ds=|d\vec{r}|$ 是正确的，出现 $\Delta r$ ， $dr$ 基本都是错的

速度：

• 平均速度 $\overline{v} = \frac{\Delta \overline{r}}{\Delta t}$，平均速率是路程除以时间 $\overline{v} = \frac{\Delta s}{\Delta t}$
• 瞬时速度就是对每个坐标分量求导 $\overline{v} = \frac{d \overline{r}}{dt} = \frac{dx}{dt} \hat{i} + \frac{dy}{dt} \hat{j} + \frac{dz}{dt} \hat{k}$
• 瞬时速率是瞬时速度的大小

$$v = \left| \frac{d \overline{r}}{dt} \right| = \frac{ds}{dt} = \sqrt{\left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2 + \left( \frac{dz}{dt} \right)^2}$$

• 注意：不能写成 $\frac{dr}{dt}$ 或 $\frac{d|\overline{r}|}{dt}$

加速度：

• 平均加速度 $\overline{a} = \frac{\Delta \overline{v}}{\Delta t}$
• 瞬时加速度就是对每个速度分量求导

$$\overline{a} = \frac{d \overline{v}}{dt} = \frac{dv_x}{dt} \hat{i} + \frac{dv_y}{dt} \hat{j} + \frac{dv_z}{dt} \hat{k}$$

• 注意：加速度与速度同号为加速、异号为减速

转换：

$$v = \frac{dx}{dt}, \quad a = \frac{dv}{dt}\\ v = v_0 + \int_0^t a \, dt, \quad x = x_0 + \int_0^t v \, dt$$

· 圆周运动参数

加速度的分解：

• 加速度可以沿速度方向分解

• 与速度方向平行的称为切向加速度，改变速度的大小 $a_t = \frac{dv}{dt}$

• 与速度方向垂直的称为法向加速度，改变速度的方向 $a_n = \frac{v^2}{\rho}$（$\rho$ 为曲率半径）

转化：

角位移： $\theta$ 角速度： $\omega$ 角加速度： $\alpha$

$$\omega = \frac{d\theta}{dt}, \quad \alpha = \frac{d\omega}{dt}, \quad \omega = \omega_0 + \int_0^t \alpha \, dt, \quad \theta = \theta_0 + \int_0^t \omega \, dt$$

角量与线量的关系：

• 线速度 $v = \omega R$

• 法向加速度 $a_n = \frac{v^2}{R} = \omega^2 R$

• 切向加速度 $a_t = \frac{dv}{dt} = \alpha R$

Fragment 1 质点

近代物理学研究的第一个课题是力学。这是由于它直接服务于战争的需要，即解释天体的运行和如何修正炮弹的弹道。为此，这一学科的研究得到了国王们的大力资助。

以天体的研究为例。天体之间的距离是如此之大，相比之下，每一个天体的直径就微不足道了。例如，太阳的直径为 $10^9$ 米，地球的直径为 $10^7$ 米，但是地球到太阳的距离为 $10^{11}$ 米。即地球轨道的半径与其自身的半径之比为 $10^{11}/10^7 = 10^4$。这就使得人们在计算地球的运动轨迹时可以暂时忽略其线度，而将其视作一个几何点。但是，我们必须将其质量考虑进来。一个具有质量的几何点加上质量，称为质点或粒子 (Particle)。

为了研究一个质点的运动，人们需要引入一个参照系。在这个参照系中，可以任取一点作为原点 $O$，然后建立合适的坐标系。自然，如果原点取得不好，质点的运动方程可能写出来很复杂。除此之外，取什么样的参照系并不是什么大不了的问题。

在取定原点之后，我们可以从原点 $O$ 到质点 $P$ 画一向量（或矢量）

$$\mathbf{r} = \overrightarrow{OP},\tag{1}$$

称为质点在该时刻的位置向量。显然，它是时间的函数，即我们有

$$\mathbf{r} = \mathbf{r}(t).\tag{2}$$

在两个相邻时刻 $t$ 和 $t + \Delta t$，粒子可能有两个不同的位置向量 $\mathbf{r}(t)$ 和 $\mathbf{r}(t + \Delta t)$。它们的差 $\Delta \mathbf{r}(t)$ 定义为

$$\Delta \mathbf{r}(t) = \mathbf{r}(t + \Delta t) - \mathbf{r}(t).\tag{3}$$

由此，我们可以定义质点在时刻 $t$ 的速度为

$$\mathbf{v}(t) \equiv \lim_{\Delta t \to 0} \frac{\Delta \mathbf{r}(t)}{\Delta t} = \frac{d\mathbf{r}}{dt} = \dot{\mathbf{r}}(t).\tag{4}$$

这是一个向量。它的绝对值

$$|\mathbf{v}| \equiv \sqrt{\mathbf{v} \cdot \mathbf{v}}\tag{5}$$

被称为质点 $P$ 在时刻 $t$ 时的速率。

同理，我们可以定义质点在 $t$ 时刻的加速度向量为

$$\mathbf{a}(t) \equiv \lim_{\Delta t \to 0} \frac{\Delta \mathbf{v}(t)}{\Delta t} = \lim_{\Delta t \to 0} \frac{\mathbf{v}(t + \Delta t) - \mathbf{v}(t)}{\Delta t} = \frac{d\mathbf{v}(t)}{dt} = \frac{d^2\mathbf{r}(t)}{dt^2}.\tag{6}$$

用矢量来描述质点运动的好处是，对于给定的参照系，矢量表示的运动方程的形式与具体的坐标系的选择无关。因此，便于我们做一般性的定义陈述和理论推导。但是，在做具体计算时，我们还需要根据问题的特点，选择适当的坐标系。

Fragment 2 坐标系

· 直角坐标系

当质点的加速度为一个常向量时，选用直角坐标系往往是适宜的。在这一坐标系中，我们在原点上建立三个互相垂直的固定坐标轴。以 $\mathbf{e}_x$, $\mathbf{e}_y$ 和 $\mathbf{e}_z$ 表示沿这三个轴方向的单位向量，则我们有

$$\mathbf{e}_x \cdot \mathbf{e}_y = \mathbf{e}_y \cdot \mathbf{e}_z = \mathbf{e}_z \cdot \mathbf{e}_x = 0,\tag{7}$$

以及

$$\mathbf{e}_x \cdot \mathbf{e}_x = \mathbf{e}_y \cdot \mathbf{e}_y = \mathbf{e}_z \cdot \mathbf{e}_z = 1.\tag{8}$$

在这一坐标系下，质点的位置向量可以被写作

$$\mathbf{r}(t) = x(t)\mathbf{e}_x + y(t)\mathbf{e}_y + z(t)\mathbf{e}_z.\tag{9}$$

而其速度和加速度向量可被分别写作

$$\begin{aligned} \mathbf{v}(t) &= \frac{d\mathbf{r}(t)}{dt} = \frac{d}{dt} (x(t)\mathbf{e}_x + y(t)\mathbf{e}_y + z(t)\mathbf{e}_z) \\ &= \left( \dot{x}(t)\mathbf{e}_x + x(t)\frac{d\mathbf{e}_x}{dt} + \dot{y}(t)\mathbf{e}_y + y(t)\frac{d\mathbf{e}_y}{dt} + \dot{z}(t)\mathbf{e}_z + z(t)\frac{d\mathbf{e}_z}{dt} \right) \\ &= \dot{x}(t)\mathbf{e}_x + \dot{y}(t)\mathbf{e}_y + \dot{z}(t)\mathbf{e}_z \equiv v_x(t)\mathbf{e}_x + v_y(t)\mathbf{e}_y + v_z(t)\mathbf{e}_z, \end{aligned}\tag{10}$$

以及

$$\begin{align*} \mathbf{a}(t) &= \frac{d\mathbf{v}(t)}{dt} = \dot{v}_x(t)\mathbf{e}_x + \dot{v}_y(t)\mathbf{e}_y + \dot{v}_z(t)\mathbf{e}_z\\ &= \frac{d^2 x(t)}{dt^2}\mathbf{e}_x + \frac{d^2 y(t)}{dt^2}\mathbf{e}_y + \frac{d^2 z(t)}{dt^2}\mathbf{e}_z\\ & \equiv a_x(t)\mathbf{e}_x + a_y(t)\mathbf{e}_y + a_z(t)\mathbf{e}_z. \end{align*}\tag{11}$$

· 例题

/example/ 在离开地面 36.0 米处，以 $v_0 = 11.8$ 米/秒 的初始速度向上抛一小球，试求抛出后 1 秒和 3 秒末小球的位置和速度，并确定小球可到达的最高位置和从抛出到落地所需的时间。

/Claim/

首先，我们建立如下的坐标系在此坐标系下，原点为小球抛出时的位置。同时，我们有

$$\mathbf{v}_0 = v_0 \mathbf{j} = 11.8 \text{m/s } \mathbf{j}.\tag{12}$$

此时地面的坐标为 $y = -36.0\text{ m}$ 。同理，在此坐标系下，重力加速度的表达式为

$$\mathbf{g} = -9.80 \text{m/s}^2 \mathbf{j}.\tag{13}$$

这是一个匀加速度问题。因此，小球位置随时间的改变规律为

$$y(t) = a + bt + ct^2.\tag{14}$$

我们的任务就是要决定这些特定常数 $a$, $b$ 和 $c$。

为此，我们首先求上式两边对于时间 $t$ 的一次导数。我们有

$$\dot{y}(t) = b + 2ct.\tag{15}$$

按照定义，这是小球在时刻 $t$ 时的速度。现在，我们再将速度对于时间 $t$ 求一次导数，得到

$$\frac{d^2 y(t)}{dt^2} = 2c.\tag{16}$$

这是小球的加速度，它等于小球的重力加速度。因此，我们有

$$c = -\frac{1}{2} \times 9.80 \text{m/s}^2 = -4.90 \text{m/s}^2.\tag{17}$$

将它代入 $\dot{y}(t)$ 的表达式后，我们得到

$$\dot{y}(t) = v(t) = b - 9.80 \, t.\tag{18}$$

特别是当 $t = 0$ 时，我们有

$$v(t = 0) = v_0 = 11.8 \, \text{m/s}.\tag{19}$$

因此，我们有

$$b = v_0 = 11.8 \, \text{m/s}.\tag{20}$$

将 $b$ 和 $c$ 代入 $y(t)$ 的表达式后，我们得到

$$y(t) = a + v_0 t - \frac{1}{2} g t^2.\tag{21}$$

由于 $y(t = 0) = 0$，我们有 $a = 0$。因此，我们最后得到

$$y(t) = v_0 t - \frac{1}{2} g t^2.\tag{22}$$

特别是，我们有

$$y(1) = v_0 - \frac{1}{2} g = 11.8 - \frac{1}{2} \times 9.80 = 6.9 \, \text{m},\\ y(3) = 3 v_0 - \frac{1}{2} g \times 3^2 = 3 \times 11.8 - \frac{9}{2} \times 9.80 = -8.7 \text{m}.\tag{23}$$

而 $v(1)$ 和 $v(3)$ 则分别为

$$\dot{y}(1) = v_0 - g = 11.8 - 9.80 = 2.0 \, \text{m/s},\\ \dot{y}(3) = v_0 - 3g = 3 \times 11.8 - 3 \times 9.80 = -17.6 \, \text{m/s}.\tag{24}$$

为了求出小球所能到达的最高点的位置，我们注意到，此时小球的速度应该为零。即我们应该有

$$\dot{y}(t_{\max}) = v_0 - g t_{\max} = 0,\tag{25}$$

或是

$$t_{\max} = \frac{v_0}{g}.\tag{26}$$

将之代入 $y(t)$ 的表达式后，我们有

$$y_{\max} = v_0 t_{\max} - \frac{1}{2} g t_{\max}^2 = \frac{v_0^2}{g} - \frac{1}{2} g \frac{v_0^2}{g^2} = \frac{1}{2} \frac{v_0^2}{g} = 7.1 \, \text{ m}.\tag{27}$$

而为了求得小球到达地面的时间，我们需要解一元二次方程

$$y(\text{ground}) = -36.0 \, \text{m} = v_0 t_e - \frac{1}{2} g t_e^2.\tag{28}$$

我们得到两个解

$$t_{e1} = 4.17 \, \text{ s} \quad \text{and} \quad t_{e2} = -1.76 \, \text{ s}.\tag{29}$$

显然，第二个解不符合题意，应该舍去。

/example/ 考虑一个弹道问题。在地球表面附近，重力加速度 $\mathbf{g}$ 可以认为是一个常向量。如我们取与地面垂直并向上方向为 $y$ 轴，则这一加速度可以被写作

$$\mathbf{g} = -g \mathbf{e}_y.\tag{30}$$

设炮弹出膛的速度为

$$\mathbf{v}_0 = v_0 \cos \theta \, \mathbf{e}_x + v_0 \sin \theta \, \mathbf{e}_y.\tag{31}$$

则在以后的时刻内，我们有

$$\frac{d\mathbf{v}}{dt} = \frac{dv_x}{dt} \mathbf{e}_x + \frac{dv_y}{dt} \mathbf{e}_y = \mathbf{g} = -g \mathbf{e}_y,\tag{32}$$

或是

$$\frac{dv_x}{dt} = 0, \quad \frac{dv_y}{dt} = -g\tag{33}$$

成立。对于这两个公式积分后，我们有

$$v_x(t) = C_1, \quad v_y(t) = -gt + C_2.\tag{34}$$

将初始值

$$v_x(t=0) = v_0 \cos \theta, \quad v_y(t=0) = v_0 \sin \theta\tag{35}$$

代入后，我们得到

$$\frac{dx}{dt} = v_x(t) = v_0 \cos \theta, \quad \frac{dy}{dt} = v_y(t) = v_0 \sin \theta - gt.\tag{36}$$

再做一次积分后，我们得到

$$x(t) = (v_0 \cos \theta) t + D_1, \quad y(t) = (v_0 \sin \theta) t - \frac{1}{2} g t^2 + D_2.\tag{37}$$

将初始条件

$$x(t=0) = 0, \quad y(t=0) = 0\tag{38}$$

代入后，我们得到

$$x(t) = v_0 \cos \theta \, t, \quad y(t) = v_0 \sin \theta \, t - \frac{1}{2} g t^2.\tag{39}$$

从第一个方程中解出时间

$$t = \frac{x}{v_0 \cos \theta}\tag{40}$$

并代入第二个方程后，我们得到

$$y(x) = v_0 \sin \theta \frac{x}{v_0 \cos \theta} - \frac{1}{2} g \left( \frac{x}{v_0 \cos \theta} \right)^2 = x \tan \theta - \frac{1}{2} g \frac{x^2}{v_0^2 \cos^2 \theta}.\tag{41}$$

这是一个抛物线方程。为了求得炮弹的射程，我们只需令 $y = 0$

$$0 = x \tan \theta - \frac{1}{2} g \frac{x^2}{v_0^2 \cos^2 \theta},\tag{42}$$

即可解出着陆点的坐标 $\tilde{x}$。这个方程有两个解

$$x_1 = 0, \quad x_2 = \tan \theta \cdot \frac{2 v_0^2 \cos^2 \theta}{g}.\tag{434}$$

显然，我们要的是第二个解

$$\tilde{x} = \tan \theta \cdot \frac{2 v_0^2 \cos^2 \theta}{g} = \frac{v_0^2}{g} \sin 2 \theta.\tag{44}$$

根据正弦函数的定义，我们看到，当 $\theta = 45^\circ$ 时，$\tilde{x}$ 取极大值

$$x_{\max} = \frac{v_0^2}{g}.\tag{45}$$

/example/ 沿光滑铁轨设置 $x$ 轴。火车以额定功率在此铁轨上行驶。它的速度 $v(t)$ 与加速度 $a(t)$ 的乘积为一常数 $C$。设在 $t = 0$ 时刻，火车的位置为 $x = 0$，速度为 $v(t=0) = v_0$。

试求速度 $v(t)$，加速度 $a(t)$ 以及位置随时间的改变 $x(t)$。并求速度 $v$ 随位置的改变 $v(x)$。

/Claim/

按照已知条件，我们有

$$C = v(t) \cdot a(t) = \dot{x} \frac{d\dot{x}}{dt} = \frac{1}{2} \frac{d\dot{x}^2}{dt} = \frac{1}{2} \frac{dv^2(t)}{dt}.\tag{46}$$

积分后，我们有

$$\int C dt = Ct + C_0 = \frac{1}{2} v^2(t).\tag{47}$$

按照初始条件，我们有 $v(t=0) = v_0$。因此，我们得到 $C_0 = \frac{1}{2} v_0^2$。代入上面的方程后，我们得到

$$v(t) = \sqrt{2Ct + v_0^2}.\tag{48}$$

现在，为了求出 $a(t)$，我们只需将 $v(t)$ 对于时间求一次导数。我们得到

$$a(t) = \dot{v}(t) = \frac{d}{dt} \sqrt{2Ct + v_0^2} = \frac{2C}{2\sqrt{2Ct + v_0^2}} = \frac{C}{\sqrt{2Ct + v_0^2}}.\tag{49}$$

而为了求得位置随时间的改变 $x(t)$，我们需要将速度 $v(t)$ 对于时间积分。

$$x(t) = \int v(t) \, dt + C_1 = \int \sqrt{2Ct + v_0^2} \, dt + C_1\\$$

$$= \frac{2}{3} (2Ct + v_0^2)^{3/2} \cdot \frac{1}{2C} + C_1 = \frac{1}{3C} (2Ct + v_0^2)^{3/2} + C_1.\tag{50}$$

由于当 $t = 0$ 时，$x = 0$。我们有

$$C_1 = -\frac{1}{3C} v_0^3.\tag{51}$$

代入 $x(t)$ 的表达式后，我们最后得到

$$x(t) = \frac{1}{3C} (2Ct + v_0^2)^{3/2} - \frac{1}{3C} v_0^3.\tag{52}$$

为了求得 $v(x)$，我们先从 $x(t)$ 的表达式中解出

$$\sqrt{2Ct + v_0^2} = \left[ 3C \left( x + \frac{1}{3C} v_0^3 \right) \right]^{1/3} = \left( 3Cx + v_0^3 \right)^{1/3}\tag{53}$$

再将它代入 $v(t)$ 的表达式。我们得到

$$v(x) = \left( 3Cx + v_0^3 \right)^{1/3}.\tag{54}$$

结束.

· 极坐标系

当质点所受到的力总是指向参照系原点时，使用所谓极坐标系是比较方便的。

首先，我们从原点 $O$ 引出一根固定的轴，称为极轴。然后再做从原点 $O$ 到质点 $P$ 的连线 $\mathbf{r}$。则质点 $P$ 的位置可以由两个参数

$$\mathbf{r} = (r, \theta).\tag{55}$$

给定。这里，$r$ 为质点到原点的距离，而 $\theta$ 则为 $\mathbf{r}$ 与极轴之间的夹角。为了计算的缘故，我们再引入两个互相垂直的单位向量。其中，$\mathbf{e}_r$ 是沿 $\mathbf{r}$ 的方向，而 $\mathbf{e}_\theta$ 则沿角度 $\theta$ 增大的方向。

需要强调一点的是，$\mathbf{e}_r$ 和 $\mathbf{e}_\theta$ 都不是常向量。因此，我们需要计算它们随时间的变化率 $\dot{\mathbf{e}}_r$ 和 $\dot{\mathbf{e}}_\theta$。首先，不难看到，我们有

$$\Delta \mathbf{e}_r(t) = \mathbf{e}_r(t + \Delta t) - \mathbf{e}_r(t) \approx 1 \cdot \Delta \theta \cdot \mathbf{e}_\theta.\tag{56}$$

因此，$\dot{\mathbf{e}}_r$ 可以被写作

$$\frac{d \mathbf{e}_r}{dt} = \lim_{\Delta t \to 0} \frac{\Delta \mathbf{e}_r}{\Delta t} = \lim_{\Delta t \to 0} \frac{\Delta \theta}{\Delta t} \cdot \mathbf{e}_\theta = \dot{\theta} \mathbf{e}_\theta.\tag{57}$$

同理，我们有

$$\Delta \mathbf{e}_\theta(t) = \mathbf{e}_\theta(t + \Delta t) - \mathbf{e}_\theta(t) \approx 1 \cdot \Delta \theta \cdot (-\mathbf{e}_r).\tag{58}$$

因此，取极限后，我们得到

$$\frac{d \mathbf{e}_\theta}{dt} = \lim_{\Delta t \to 0} \frac{\Delta \mathbf{e}_\theta}{\Delta t} = \lim_{\Delta t \to 0} \frac{\Delta \theta}{\Delta t} \cdot (-\mathbf{e}_r) = -\dot{\theta} \mathbf{e}_r.\tag{59}$$

这两个公式是我们今后常要用到的。

现在，我们可以将质点速度和加速度向量在极坐标下的形式写出。它们分别为

$$\mathbf{v} = \dot{\mathbf{r}} = \frac{d}{dt} (r \mathbf{e}_r) = \dot{r} \mathbf{e}_r + r \dot{\mathbf{e}}_r = \dot{r} \mathbf{e}_r + r \dot{\theta} \mathbf{e}_\theta.\tag{60}$$

以及

$$\begin{align*} \mathbf{a}& = \dot{\mathbf{v}} = \frac{d}{dt} \left( \dot{r} \mathbf{e}_r + r \dot{\theta}\right)\\ &= \left( \frac{d^2r}{dt^2} \mathbf{e}_r + \dot{r} \mathbf{\hat{e}}_r + \dot{r}\dot{\theta} \mathbf{e}_{\theta} + r \frac{d^2\theta}{dt^2} \mathbf{e}_{\theta} + r \dot{\theta} \mathbf{\hat{e}}_{\theta} \right)\\ &= \left( \frac{d^2r}{dt^2} \mathbf{e}_r + \dot{r}\dot{\theta} \mathbf{e}_{\theta} + \dot{r}\dot{\theta} \mathbf{e}_{\theta} + r \frac{d^2\theta}{dt^2} \mathbf{e}_{\theta} - r \dot{\theta}^2 \mathbf{e}_r \right)\\ &= \left( \frac{d^2r}{dt^2} - r \dot{\theta}^2 \right) \mathbf{e}_r + \left( 2 \dot{r} \dot{\theta} + r \frac{d^2\theta}{dt^2} \right) \mathbf{e}_{\theta}. \end{align*}\tag{61}$$

这些表达式中，$\mathbf{e}_r$ 方向的分量被称为径向速度和径向加速度。而 $\mathbf{e}_{\theta}$ 方向的分量则被称为横向速度和横向加速度。同时，$\dot{\theta}$ 和 $\frac{d^2\theta}{dt^2}$ 被称为质点的角速度和角加速度。

· 例题

/example/

在离地面不远处，一个质点运动的加速度是指向地心的。当该质点的横向速度为何时，它做一圆周运动，从而成为地球的卫星？

/solution/

当质点做匀速圆周运动时，其横向加速度 $a_{\theta}$ 为零，而其径向加速度为

$$\mathbf{a} = \mathbf{g} = -g \mathbf{e}_r.\tag{62}$$

因此，在以地心为原点的极坐标系中，我们有

$$\frac{d^2r}{dt^2} - r \dot{\theta}^2 = -g, \quad r \frac{d^2\theta}{dt^2} + 2 \dot{r} \dot{\theta} = 0.\tag{63}$$

特别是，在这一运动中，$r = R$ 为一常数。因此上式中，$r$ 对于时间的一次和二次导数皆为零。故上式退化为

$$R \dot{\theta}^2 = g, \quad R \frac{d^2\theta}{dt^2} = 0.\tag{64}$$

从第二个方程中，我们解得

$$\dot{\theta} = constant.\tag{65}$$

从第一个方程中，我们得到

$$\frac{(R \dot{\theta})^2}{R} = g.\tag{66}$$

又由于 $R \dot{\theta}$ 为质点绕地球运动的横向速度 $v_{\theta}$ 。因此，我们最后得到

$$v_{\theta}^2 = gR,\tag{67}$$

或是

$$v_{\theta} = \sqrt{gR}.\tag{68}$$

将

$$g = 980 \, \text{cm/s}^2, \quad R \approx 6.37 \times 10^8 \, \text{cm}\tag{69}$$

代入上面的方程后，我们得到

$$v_{\theta} = \sqrt{980 \times 6.37 \times 10^8} \approx \sqrt{64 \times 10^{10}} = 8 \times 10^5 \, \text{cm/s} = 8 \, \text{km/s}\tag{70}$$

这一速度称为第一宇宙速度。

/example/ 狐狸沿半径为 $R$ 的圆轨道以恒定速率奔跑。在它出发的同时，猎犬从圆心出发以相同的速率 $v$ 追击。在此过程中，圆心，猎犬和狐狸始终连成一条直线。取圆心为原点，从圆心到狐狸的初始位置的连线为极轴，建立极坐标。

1. 试导出猎犬的速度分量 $v_r, v_{\theta}$ 和加速度分量 $a_r, a_{\theta}$ 对其坐标 $r, \theta$ 的依赖关系；
2. 确定猎犬运动轨迹的极坐标方程，并画出轨道曲线；
3. 判断猎犬能否追上狐狸。

/solution/

按照题给，在任一时刻，圆心，猎犬和狐狸始终连成一条直线。因此，猎犬和狐狸的角速度始终是一样的。故我们有

$$\dot{\theta} = \omega = \frac{v}{R}.\tag{71}$$

将此式两边同乘 $r$ 后，我们得到

$$v_{\theta} = r \dot{\theta} = r \omega = r \frac{v}{R}.\tag{72}$$

另一方面，我们又有

$$\sqrt{v_r^2 + v_{\theta}^2} = v.\tag{73}$$

因此，我们得到

$$v_r = \sqrt{v^2 - v_{\theta}^2} = \sqrt{v^2 - \frac{v^2}{R^2} r^2} = v \sqrt{1 - \frac{r^2}{R^2}}.\tag{74}$$

这样，我们就得到了 $v_r$ 与 $v_{\theta}$ 的表达式。

下面，我们求加速度 $a_r$ 和 $a_{\theta}$ 。首先，我们有

$$\begin{align*} a_r &= \frac{d^2 r}{dt^2} - r \dot{\theta}^2 = \frac{d}{dt} \left( v \sqrt{1 - \frac{r^2}{R^2}} \right) - r \left( \frac{v}{R} \right)^2\\ &= \frac{v}{2\sqrt{1-\frac{r^2}{R^2}}} \cdot \frac{(-2r\dot{r})}{R^2} - r\frac{v^2}{R^2}\\ &= -\frac{vr}{R^2\sqrt{1-\frac{r^2}{R^2}}}v_r - r\frac{v^2}{R^2}\\ &= -\frac{vr}{R^2\sqrt{1-\frac{r^2}{R^2}}} \cdot v\sqrt{1-\frac{r^2}{R^2}} - r\frac{v^2}{R^2}\\ &= -\frac{v^2r}{R^2} - r\frac{v^2}{R^2} = -2r\frac{v^2}{R^2} \end{align*}\tag{75}$$

以及

$$a_\theta = 2\dot{r}\dot{\theta} + r\frac{d^2\theta}{dt^2} = 2v_r\dot{\theta} = 2v_r\omega = 2v\sqrt{1-\frac{r^2}{R^2}} \cdot \frac{v}{R} = 2\frac{v^2}{R}\sqrt{1-\frac{r^2}{R^2}}.\tag{76}$$

为了求得猎犬运动轨迹的曲线，我们可以先计算 $\frac{dr}{d\theta}$ 。我们有

$$\frac{dr}{d\theta} = \frac{dr}{dt} \cdot \frac{dt}{d\theta} = v_r \frac{1}{\left(\frac{d\theta}{dt}\right)} = v\sqrt{1-\frac{r^2}{R^2}} \frac{1}{\omega} = v\sqrt{1-\frac{r^2}{R^2}} \cdot \frac{R}{v} = \sqrt{R^2 - r^2}.\tag{77}$$

由此，我们得到

$$\int \frac{dr}{\sqrt{R^2 - r^2}} = \arcsin\frac{r}{R} = \int d\theta + C = \theta + C.\tag{78}$$

由于 $\theta = 0$ 时， $r = 0$ 。我们有 $C = 0$ 。代入上式后，我们得到

$$r = R \sin \theta.\tag{79}$$

这就是猎犬所走的路径。我们看到，当 $\theta = \frac{\pi}{2}$ 时， $r = R$ 。因此，猎犬在此处追上狐狸。

· 自然坐标系

在理论推导中，采用所谓自然坐标系常会带来很大的便利。我们今后也会经常用到它。

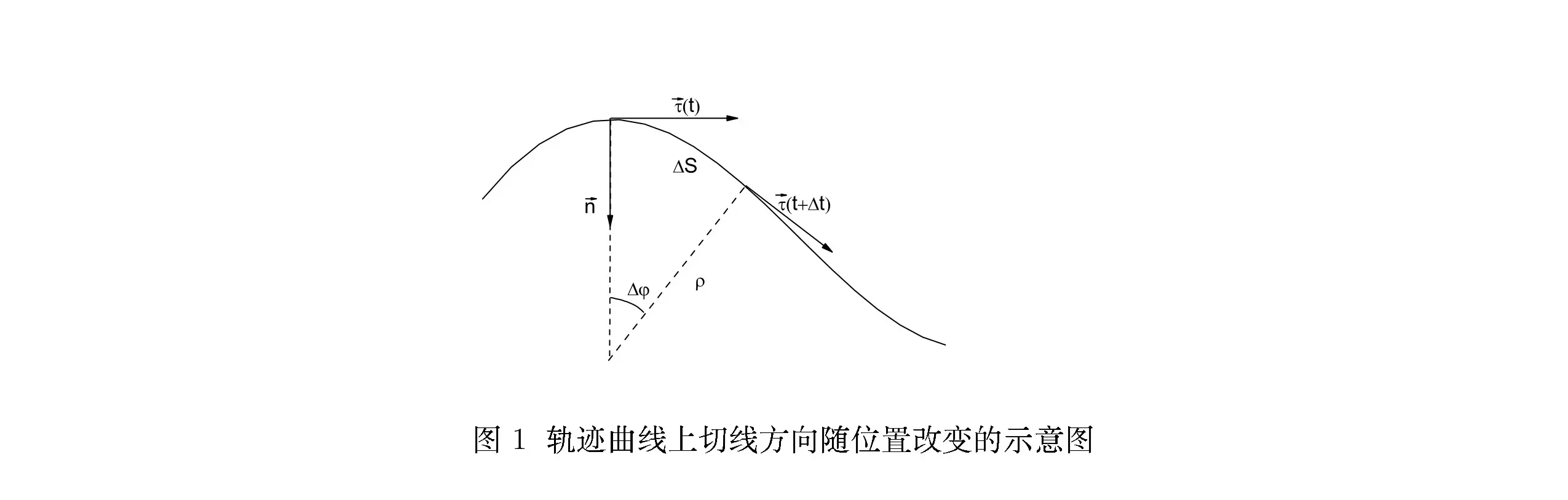
如图所示，我们先取质点运动轨迹上的任一点作为起始位置，对应的时间为 $t = 0$ 。

在此之后 $(t > 0)$ ，质点所到达的任何一点 $P$ 的坐标由其从起始点算起的弧长 $s$ 决定。

在 $P$ 点处，我们可以取曲线的切线方向的单位向量 $\vec{\tau}$ 和内法线方向单位向量 $\vec{n}$ 。它们就定义了所谓自然坐标系。

显然，这样定义的 $\vec{\tau}$ 和 $\vec{n}$ 都不是常向量。在轨迹的不同位置，我们有不同的 $\vec{\tau}$ 和 $\vec{n}$ 。

设在 $t$ 和 $t + \Delta t$ 时刻，质点的位置分别为 $\mathbf{r}(t)$ 及 $\mathbf{r}(t + \Delta t)$ 。而它们对应的从起始点计算的弧长为 $s(t)$ 和 $s(t + \Delta t)$ ，并且两点间的向量差为 $\Delta \mathbf{r}$ 。则从微分几何学中，我们知道

$$\vec{\tau} = \lim_{\Delta s \to 0} \frac{\Delta \vec{\tau}}{\Delta s} = \frac{d\mathbf{r}}{ds}\tag{80}$$

成立。进一步，我们还有

$$\frac{d\vec{\tau}}{ds} = \lim_{\Delta s \to 0} \frac{\Delta \vec{\tau}}{\Delta s} = \lim_{\Delta s \to 0} \frac{\Delta \vec{\tau}}{\Delta \varphi} \cdot \lim_{\Delta s \to 0} \frac{\Delta \varphi}{\Delta s} = \frac{1}{\rho} \vec{n}.\tag{81}$$

这里， $\rho$ 称为曲线在 $\mathbf{r}$ 处的密切圆曲率半径。在图1中，我们给出了这些几何关系的一个示意图。下面，我们还要用到它们。

现在，让我们回过头来看一下，质点随时间改变的速度和加速度如何在自然坐标系中给出。

按照定义，我们有

$$\mathbf{v} = \frac{d\mathbf{r}}{dt} = \frac{d\mathbf{r}}{ds} \cdot \frac{ds}{dt} = \frac{ds}{dt} \vec{\tau} = v \vec{\tau}.\tag{82}$$

这里， $v$ 称为质点的切向速率。从上式中我们可以看到，质点的速度永远是沿着切线方向的。

至于加速度 $\mathbf{a}$ ，我们可以计算如下。

$$\mathbf{a} = \frac{d\mathbf{v}}{dt} = \frac{d}{dt}(v\vec{\tau}) = \frac{dv}{dt}\vec{\tau} + v\frac{d\vec{\tau}}{dt}$$

$$= \frac{dv}{dt}\vec{\tau} + v\frac{d\vec{\tau}}{ds} \cdot \frac{ds}{dt} = \frac{dv}{dt}\vec{\tau} + v \cdot \frac{v}{\rho} \vec{n}$$

$$= \frac{dv}{dt}\vec{\tau} + \frac{v^2}{\rho} \vec{n} \equiv a_\tau \vec{\tau} + a_n \vec{n}.\tag{83}$$

这里，

$$a_\tau = \frac{dv}{dt}, \quad a_n = \frac{v^2}{\rho}\tag{84}$$

分别为质点的切向和法向加速度分量。

· 例题

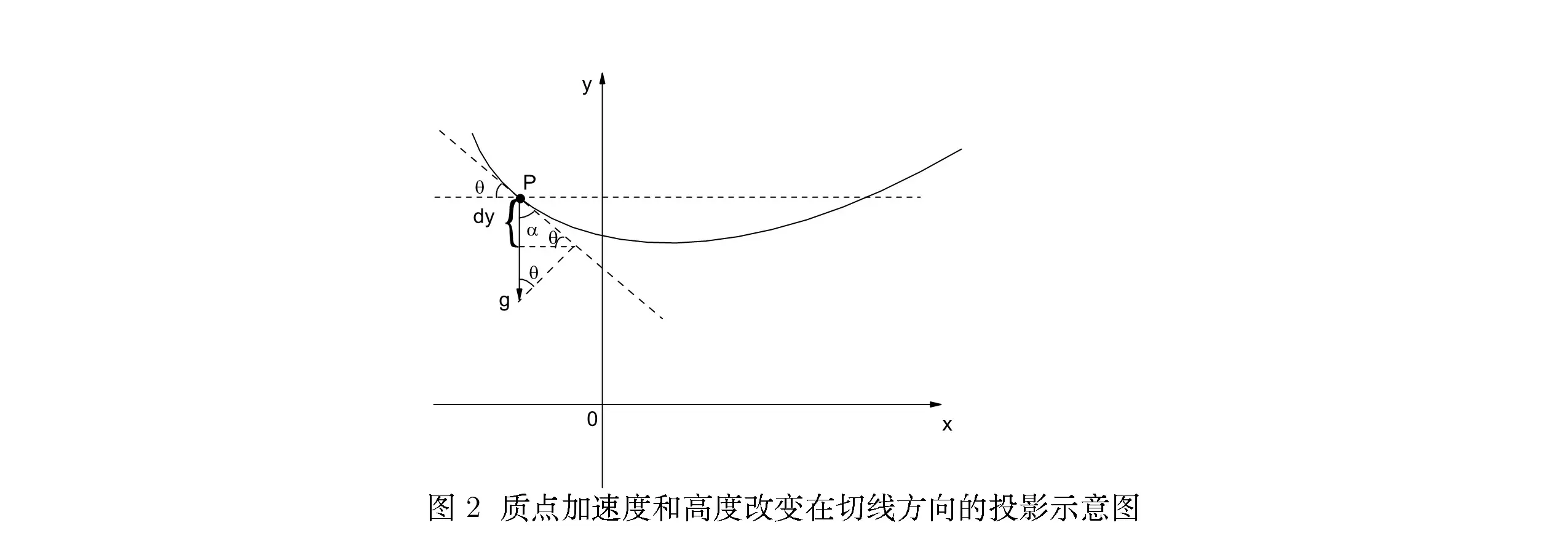
/example/ 如图2所示，质点沿由光滑的钢丝弯成的一条在竖直平面内的曲线运动。已知质点的切向加速度为 $a_\tau = g \sin \theta$ 。试求其在钢丝各点处的运动速率 $v$ 。

/solution/

按照自然坐标中，切向加速度的定义，我们有

$$a_\tau = \frac{dv_\tau}{dt} = \frac{dv}{dt} = g \sin \theta.\tag{85}$$

另一方面，我们知道

$$v = v_\tau = \frac{ds}{dt}\tag{86}$$

以及

$$\frac{dy}{ds} = -\sin\theta. \tag{87}$$

因此，我们有

$$\frac{dv}{dt} = \frac{dv}{dy} \cdot \frac{dy}{ds} \cdot \frac{ds}{dt} = \frac{dv}{dy} \cdot (-\sin\theta) \cdot v. \tag{88}$$

将它代入方程 (85) 的左边后，我们得到

$$-\frac{dv}{dy} \cdot \sin\theta \cdot v = g \sin\theta. \tag{89}$$

方程两边同时除以 $\sin\theta$ 后，我们得到

$$\frac{dv}{dy} \cdot v = -g, \tag{90}$$

或是

$$v dv = -g dy. \tag{91}$$

积分后，我们得到

$$\frac{1}{2} v^2 = -gy + C. \tag{92}$$

若令 $v(y = y_0) = v_0$ ，则我们可以定出常数 $C$ 。我们有

$$C = \frac{1}{2} v_0^2 + gy_0. \tag{93}$$

代入上式后，我们最后得到

$$v^2 - v_0^2 = 2g(y_0 - y). \tag{94}$$

/example/ 质点沿半长轴为 $A$ ，半短轴为 $B$ 的椭圆轨道运动，速率为常数 $v$ 。试求质点在两个端点处的加速度 $a_A$ 和 $a_B$ 。

/solution/

按照题意，质点在椭圆任何一点处的切线加速度 $a_\tau = \dot{v} = 0$ 皆为零。因此，我们只需求质点在两个端点处的法向加速度

$$a_n(A) = \frac{v^2}{\rho_A}, \quad a_n(B) = \frac{v^2}{\rho_B} \tag{95}$$

即可。

为了求出密切圆半径 $\rho_A$ 和 $\rho_B$ ，我们可以假想质点满足如下两个条件的运动。一是它的运动轨迹仍然为同一椭圆，二是应该使得我们能够比较容易地决定它在各点处的速度和法向加速度，以便决定相应的密切圆半径。

我们知道，圆是椭圆的一个特例。对于一个在给定的半径为 $R$ 的圆上运动的质点而言，若我们取

$$x(t) = R \cos \omega t, \quad y(t) = R \sin \omega t, \tag{96}$$

则它的运动轨迹即是下式

$$x^2 + y^2 = R^2 \tag{97}$$

所代表的圆。类似地，若我们假设质点轨迹的随时间的改变分别为

$$x(t) = A \cos \omega t, \quad y(t) = B \sin \omega t, \tag{98}$$

则其运动轨迹的方程为椭圆

$$\frac{x^2}{A^2} + \frac{y^2}{B^2} = 1. \tag{99}$$

特别是，端点 $A$ 和 $B$ 分别对应于

$$\omega t = 0, \quad \text{and} \quad \omega t = \frac{\pi}{2}. \tag{100}$$

由此质点运动轨迹坐标的表达式，我们可得其速度表达式

$$v_x(t) = \dot{x}(t) = -A\omega \sin \omega t, \quad v_y(t) = \dot{y}(t) = B\omega \cos \omega t, \tag{101}$$

和加速度的表达式

$$a_x(t) = \dot{v}_x(t) = -A\omega^2 \cos \omega t, \quad a_y(t) = \dot{v}_y(t) = -B\omega^2 \sin \omega t \tag{102}$$

特别是在 $A$ 点，我们有

$$v_x(\omega t = 0) = 0, \quad v_y(\omega t = 0) = B\omega, \quad a_x(\omega t = 0) = -A\omega^2, \quad a_y(\omega t = 0) = 0. \tag{103}$$

因此，在该处，质点的速度平方为

$$v_A^2 = B^2 \omega^2, \tag{104}$$

而法向加速度为

$$a_n(A) = |a_x(A)| = A\omega^2. \tag{105}$$

由此，我们得到该点处密切圆半径为

$$\rho_A = \frac{v_A^2}{a_n(A)} = \frac{B^2\omega^2}{A\omega^2} = \frac{B^2}{A}. \tag{106}$$

同理，在端点 $B$ 处，我们有

$$v_x\left(\omega t = \frac{\pi}{2}\right) = -A\omega, \quad v_y\left(\omega t = \frac{\pi}{2}\right) = 0,$$

$$a_x\left(\omega t = \frac{\pi}{2}\right) = 0, \quad a_y\left(\omega t = \frac{\pi}{2}\right) = -B\omega^2. \tag{107}$$

因此，我们得到该点处密切圆半径为

$$\rho_B = \frac{v_B^2}{a_n(B)} = \frac{A^2\omega^2}{B\omega^2} = \frac{A^2}{B}. \tag{108}$$

在求得了 $\rho_A$ 和 $\rho_B$ 之后，我们现在可以直接来确定作匀速运动的质点在这些点处的法向加速度了。它们分别为

$$a_n(A) = \frac{v^2}{\rho_A} = \frac{Av^2}{B^2}, \quad a_n(B) = \frac{v^2}{\rho_B} = \frac{Bv^2}{A^2}. \tag{109}$$

Fragment 3 相对运动

· 伽利略变换

在实际工作中，如何选取参照系往往是由观察环境决定的。例如，为了描述太阳系中物体的运动，最好选取太阳为坐标的原点。然而，为了描述地球上的一辆汽车或一艘轮船的运动，这样的选取显然是不明智的。此时，我们最好选取地球上的一个固定点，例如地心作为原点。这样，就导致了一个间题，即如何在两个不同的参照系中，描述同一个物体的运动。

为了回答这一问题，让我们考虑如下的例子。假设一个参照系 $S'$ 相对于另外一个参照系 $S$ 做运动。而空间中又有一个质点 $P$ 相对于二者运动。显然，我们有